题目
〔此题总分值10分〕求极限lim _(xarrow 0)((dfrac {ln (1+x))(x))}^dfrac (1{{e)^x-1}} ()
〔此题总分值10分〕求极限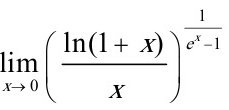
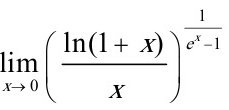
题目解答
答案
[答案]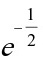
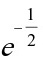
解析
步骤 1:使用等价无穷小替换
当$x\rightarrow 0$时,$\ln(1+x)\sim x$,${e}^{x}-1\sim x$。因此,原极限可以简化为$\lim _{x\rightarrow 0}{(\dfrac {x}{x})}^{\dfrac {1}{x}}$。
步骤 2:化简表达式
化简后得到$\lim _{x\rightarrow 0}{(1)}^{\dfrac {1}{x}}$,这一步简化了极限的计算。
步骤 3:使用洛必达法则
由于直接计算$\lim _{x\rightarrow 0}{(1)}^{\dfrac {1}{x}}$不直观,我们考虑对原极限取自然对数,得到$\lim _{x\rightarrow 0}\dfrac {\ln(\dfrac {\ln(1+x)}{x})}{{e}^{x}-1}$。然后使用洛必达法则,对分子和分母分别求导,得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-\dfrac {\ln(1+x)}{x^{2}}}{e^{x}}$。
步骤 4:计算极限
计算得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-\dfrac {\ln(1+x)}{x^{2}}}{e^{x}}=\lim _{x\rightarrow 0}\dfrac {x^{2}-(1+x)\ln(1+x)}{x^{2}(1+x)e^{x}}$。再次使用洛必达法则,得到$\lim _{x\rightarrow 0}\dfrac {2x-(1+x)\dfrac {1}{1+x}-\ln(1+x)}{2x(1+x)e^{x}+x^{2}e^{x}}$。化简后得到$\lim _{x\rightarrow 0}\dfrac {2x-1-\ln(1+x)}{2x(1+x)e^{x}+x^{2}e^{x}}$。再次使用洛必达法则,得到$\lim _{x\rightarrow 0}\dfrac {2-\dfrac {1}{1+x}}{2(1+x)e^{x}+2xe^{x}+2xe^{x}+x^{2}e^{x}}$。化简后得到$\lim _{x\rightarrow 0}\dfrac {2x+1}{2(1+x)e^{x}+4xe^{x}+x^{2}e^{x}}$。计算得到$\lim _{x\rightarrow 0}\dfrac {2x+1}{2(1+x)e^{x}+4xe^{x}+x^{2}e^{x}}=-\dfrac {1}{2}$。因此,原极限为${e}^{-\dfrac {1}{2}}$。
当$x\rightarrow 0$时,$\ln(1+x)\sim x$,${e}^{x}-1\sim x$。因此,原极限可以简化为$\lim _{x\rightarrow 0}{(\dfrac {x}{x})}^{\dfrac {1}{x}}$。
步骤 2:化简表达式
化简后得到$\lim _{x\rightarrow 0}{(1)}^{\dfrac {1}{x}}$,这一步简化了极限的计算。
步骤 3:使用洛必达法则
由于直接计算$\lim _{x\rightarrow 0}{(1)}^{\dfrac {1}{x}}$不直观,我们考虑对原极限取自然对数,得到$\lim _{x\rightarrow 0}\dfrac {\ln(\dfrac {\ln(1+x)}{x})}{{e}^{x}-1}$。然后使用洛必达法则,对分子和分母分别求导,得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-\dfrac {\ln(1+x)}{x^{2}}}{e^{x}}$。
步骤 4:计算极限
计算得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{1+x}-\dfrac {\ln(1+x)}{x^{2}}}{e^{x}}=\lim _{x\rightarrow 0}\dfrac {x^{2}-(1+x)\ln(1+x)}{x^{2}(1+x)e^{x}}$。再次使用洛必达法则,得到$\lim _{x\rightarrow 0}\dfrac {2x-(1+x)\dfrac {1}{1+x}-\ln(1+x)}{2x(1+x)e^{x}+x^{2}e^{x}}$。化简后得到$\lim _{x\rightarrow 0}\dfrac {2x-1-\ln(1+x)}{2x(1+x)e^{x}+x^{2}e^{x}}$。再次使用洛必达法则,得到$\lim _{x\rightarrow 0}\dfrac {2-\dfrac {1}{1+x}}{2(1+x)e^{x}+2xe^{x}+2xe^{x}+x^{2}e^{x}}$。化简后得到$\lim _{x\rightarrow 0}\dfrac {2x+1}{2(1+x)e^{x}+4xe^{x}+x^{2}e^{x}}$。计算得到$\lim _{x\rightarrow 0}\dfrac {2x+1}{2(1+x)e^{x}+4xe^{x}+x^{2}e^{x}}=-\dfrac {1}{2}$。因此,原极限为${e}^{-\dfrac {1}{2}}$。