题目
求过直线 {z)^2 x+y+2z=4. . 在点 (1,-1,2) 处的切线平行的平面方程.
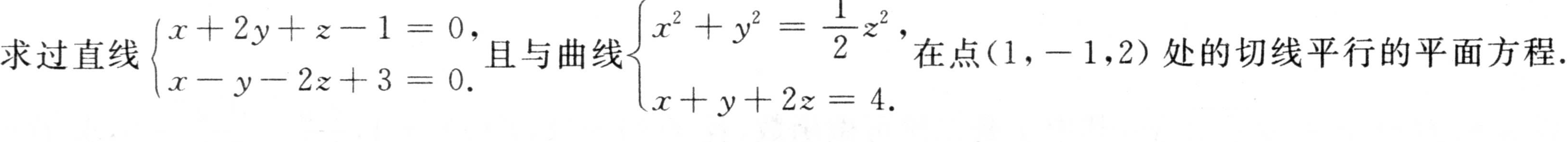
题目解答
答案

解析
步骤 1:求曲线在点 (1,-1,2) 处的切向量
曲线 $\left \{ \begin{matrix} {x}^{2}+{y}^{2}=\dfrac {1}{2}{z}^{2}\\ x+y+2z=4\end{matrix} \right.$ 在点 (1,-1,2) 处的切向量可以通过计算两个曲面的法向量的叉积得到。第一个曲面的法向量为 $\nabla F_1 = (2x, 2y, -z)$,第二个曲面的法向量为 $\nabla F_2 = (1, 1, 2)$。在点 (1,-1,2) 处,$\nabla F_1 = (2, -2, -2)$,$\nabla F_2 = (1, 1, 2)$。因此,切向量为 $\nabla F_1 \times \nabla F_2 = \left |\begin{matrix} i& j& k\\ 2& -2& -2\\ 1& 1& 2\end{matrix} \right | = (-2,-6,4)$。
步骤 2:求过直线的平面束方程
过直线 $\left \{ \begin{matrix} x+2y+z-1=0\\ x-y-2z+3=0\end{matrix} \right.$ 的平面束方程为 $x+2y+z-1+\lambda (x-y-2z+3)=0$。将切向量 $(-2,-6,4)$ 代入平面束方程,得到 $-2+2(-6)+4-1+\lambda (-2-(-6)-2(4)+3)=0$,解得 $\lambda =-\dfrac {5}{2}$。
步骤 3:求所求平面方程
将 $\lambda =-\dfrac {5}{2}$ 代入平面束方程,得到 $x+2y+z-1-\dfrac {5}{2}(x-y-2z+3)=0$,化简得到 $3x-9y-12z+17=0$。
曲线 $\left \{ \begin{matrix} {x}^{2}+{y}^{2}=\dfrac {1}{2}{z}^{2}\\ x+y+2z=4\end{matrix} \right.$ 在点 (1,-1,2) 处的切向量可以通过计算两个曲面的法向量的叉积得到。第一个曲面的法向量为 $\nabla F_1 = (2x, 2y, -z)$,第二个曲面的法向量为 $\nabla F_2 = (1, 1, 2)$。在点 (1,-1,2) 处,$\nabla F_1 = (2, -2, -2)$,$\nabla F_2 = (1, 1, 2)$。因此,切向量为 $\nabla F_1 \times \nabla F_2 = \left |\begin{matrix} i& j& k\\ 2& -2& -2\\ 1& 1& 2\end{matrix} \right | = (-2,-6,4)$。
步骤 2:求过直线的平面束方程
过直线 $\left \{ \begin{matrix} x+2y+z-1=0\\ x-y-2z+3=0\end{matrix} \right.$ 的平面束方程为 $x+2y+z-1+\lambda (x-y-2z+3)=0$。将切向量 $(-2,-6,4)$ 代入平面束方程,得到 $-2+2(-6)+4-1+\lambda (-2-(-6)-2(4)+3)=0$,解得 $\lambda =-\dfrac {5}{2}$。
步骤 3:求所求平面方程
将 $\lambda =-\dfrac {5}{2}$ 代入平面束方程,得到 $x+2y+z-1-\dfrac {5}{2}(x-y-2z+3)=0$,化简得到 $3x-9y-12z+17=0$。