题目
判定下列级数的收敛性: (1)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···; (2)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···; (3)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···; (4)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···; (5)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···; (6)dfrac (3)(4)+2((dfrac {3)(4))}^2+3((dfrac {3)(4))}^3+... +n((dfrac {3)(4))}^n+... )^n+···.
判定下列级数的收敛性:
(1)![]() ;
;
(2)![]() ;
;
(3)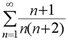 ;
;
(4)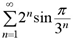 ;
;
(5)![]() ;
;
(6)![]() .
.
题目解答
答案
解(1) 这里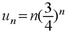 , 因为
, 因为
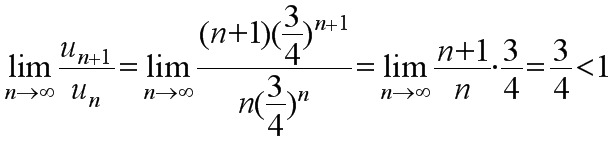 ,
,
所以级数收敛.
(2) 这里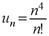 , 因为
, 因为
![]() ,
,
所以级数收敛.
(3) 因为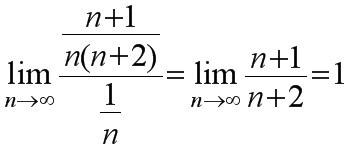 , 而级数
, 而级数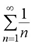 发散,
发散,
故所给级数发散.
(4) 因为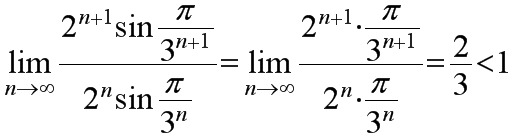 ,
,
所以级数收敛.
(5) 因为![]() ,
,
所以级数发散.
(6) 因为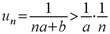 , 而级数
, 而级数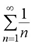 发散,
发散,
故所给级数发散.
解析
步骤 1:确定通项
级数的通项为 ${u}_{n}=n{(\dfrac {3}{4})}^{n}$。
步骤 2:应用比值判别法
计算 $\lim _{n\rightarrow \infty }\dfrac {{u}_{n+1}}{{u}_{n}}$,即
$\lim _{n\rightarrow \infty }\dfrac {(n+1){(\dfrac {3}{4})}^{n+1}}{n{(\dfrac {3}{4})}^{n}}=\lim _{n\rightarrow \infty }\dfrac {3}{4}\cdot \dfrac {n+1}{n}=\dfrac {3}{4}\lt 1$。
步骤 3:判断收敛性
由于比值小于1,根据比值判别法,级数收敛。
【答案】
级数收敛。
(2) 判定级数 $\dfrac {{1}^{4}}{1!}+\dfrac {{2}^{4}}{2!}+\dfrac {{3}^{4}}{3!}+\cdots +\dfrac {{n}^{4}}{n!}+\cdots $ 的收敛性。
【解析】
步骤 1:确定通项
级数的通项为 ${u}_{n}=\dfrac {{n}^{4}}{n!}$。
步骤 2:应用比值判别法
计算 $\lim _{n\rightarrow \infty }\dfrac {{u}_{n+1}}{{u}_{n}}$,即
$\lim _{n\rightarrow \infty }\dfrac {{(n+1)}^{4}}{(n+1)!}\cdot \dfrac {n!}{{n}^{4}}=\lim _{n\rightarrow \infty }\dfrac {1}{n}\cdot {(\dfrac {n+1}{n})}^{4}=0$。
步骤 3:判断收敛性
由于比值为0,根据比值判别法,级数收敛。
【答案】
级数收敛。
(3) 判定级数 $\sum _{n=1}^{\infty }\dfrac {n+1}{n(n+2)}$ 的收敛性。
【解析】
步骤 1:确定通项
级数的通项为 ${u}_{n}=\dfrac {n+1}{n(n+2)}$。
步骤 2:应用比较判别法
比较 ${u}_{n}$ 与 $\dfrac {1}{n}$,因为 $\lim _{n\rightarrow \infty }\dfrac {n+1}{n(n+2)}\cdot n=\lim _{n\rightarrow \infty }\dfrac {n+1}{n+2}=1$,而级数 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,所以级数 $\sum _{n=1}^{\infty }\dfrac {n+1}{n(n+2)}$ 发散。
级数的通项为 ${u}_{n}=n{(\dfrac {3}{4})}^{n}$。
步骤 2:应用比值判别法
计算 $\lim _{n\rightarrow \infty }\dfrac {{u}_{n+1}}{{u}_{n}}$,即
$\lim _{n\rightarrow \infty }\dfrac {(n+1){(\dfrac {3}{4})}^{n+1}}{n{(\dfrac {3}{4})}^{n}}=\lim _{n\rightarrow \infty }\dfrac {3}{4}\cdot \dfrac {n+1}{n}=\dfrac {3}{4}\lt 1$。
步骤 3:判断收敛性
由于比值小于1,根据比值判别法,级数收敛。
【答案】
级数收敛。
(2) 判定级数 $\dfrac {{1}^{4}}{1!}+\dfrac {{2}^{4}}{2!}+\dfrac {{3}^{4}}{3!}+\cdots +\dfrac {{n}^{4}}{n!}+\cdots $ 的收敛性。
【解析】
步骤 1:确定通项
级数的通项为 ${u}_{n}=\dfrac {{n}^{4}}{n!}$。
步骤 2:应用比值判别法
计算 $\lim _{n\rightarrow \infty }\dfrac {{u}_{n+1}}{{u}_{n}}$,即
$\lim _{n\rightarrow \infty }\dfrac {{(n+1)}^{4}}{(n+1)!}\cdot \dfrac {n!}{{n}^{4}}=\lim _{n\rightarrow \infty }\dfrac {1}{n}\cdot {(\dfrac {n+1}{n})}^{4}=0$。
步骤 3:判断收敛性
由于比值为0,根据比值判别法,级数收敛。
【答案】
级数收敛。
(3) 判定级数 $\sum _{n=1}^{\infty }\dfrac {n+1}{n(n+2)}$ 的收敛性。
【解析】
步骤 1:确定通项
级数的通项为 ${u}_{n}=\dfrac {n+1}{n(n+2)}$。
步骤 2:应用比较判别法
比较 ${u}_{n}$ 与 $\dfrac {1}{n}$,因为 $\lim _{n\rightarrow \infty }\dfrac {n+1}{n(n+2)}\cdot n=\lim _{n\rightarrow \infty }\dfrac {n+1}{n+2}=1$,而级数 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,所以级数 $\sum _{n=1}^{\infty }\dfrac {n+1}{n(n+2)}$ 发散。