题目
极限lim _(xarrow infty )(x)^2(2-xsin dfrac (1)(x)-cos dfrac (1)(x))=A.lim _(xarrow infty )(x)^2(2-xsin dfrac (1)(x)-cos dfrac (1)(x))=B.lim _(xarrow infty )(x)^2(2-xsin dfrac (1)(x)-cos dfrac (1)(x))=C.lim _(xarrow infty )(x)^2(2-xsin dfrac (1)(x)-cos dfrac (1)(x))=D.lim _(xarrow infty )(x)^2(2-xsin dfrac (1)(x)-cos dfrac (1)(x))=
极限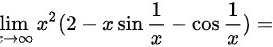
A.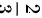
B.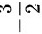
C.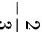
D.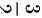
题目解答
答案
∵当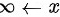 时,
时,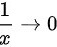 ,
,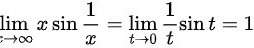
∴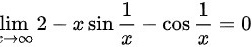
∴对于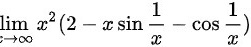 ,可以令
,可以令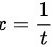 (洛必达更方便)
(洛必达更方便)
则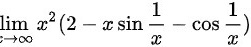
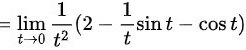
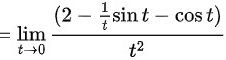
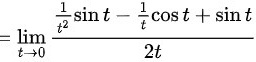
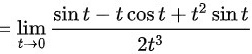
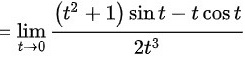
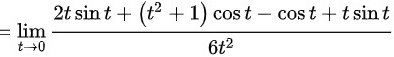
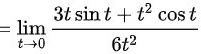
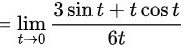
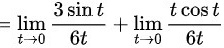
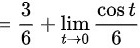
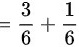
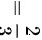
∴综上所述,极限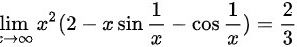
故选A
解析
步骤 1:确定极限形式
首先,我们观察到当$x\rightarrow \infty$时,$\dfrac{1}{x}\rightarrow 0$。因此,我们需要计算$\lim _{x\rightarrow \infty }{x}^{2}(2-x\sin \dfrac {1}{x}-\cos \dfrac {1}{x})$,这可以转换为$\lim _{t\rightarrow 0}\dfrac {1}{{t}^{2}}(2-\dfrac {1}{t}\sin t-\cos t)$,其中$t=\dfrac{1}{x}$。
步骤 2:应用洛必达法则
由于直接计算上述极限比较困难,我们应用洛必达法则。洛必达法则适用于$\dfrac{0}{0}$或$\dfrac{\infty}{\infty}$形式的极限。因此,我们有:
$$\lim _{t\rightarrow 0}\dfrac {1}{{t}^{2}}(2-\dfrac {1}{t}\sin t-\cos t) = \lim _{t\rightarrow 0}\dfrac {2-\dfrac {1}{t}\sin t-\cos t}{{t}^{2}}$$
应用洛必达法则,我们对分子和分母同时求导:
$$\lim _{t\rightarrow 0}\dfrac {2-\dfrac {1}{t}\sin t-\cos t}{{t}^{2}} = \lim _{t\rightarrow 0}\dfrac {\dfrac{d}{dt}(2-\dfrac {1}{t}\sin t-\cos t)}{\dfrac{d}{dt}({t}^{2})}$$
$$= \lim _{t\rightarrow 0}\dfrac {\dfrac{1}{t^2}\sin t - \dfrac{1}{t}\cos t + \sin t}{2t}$$
$$= \lim _{t\rightarrow 0}\dfrac {\sin t - t\cos t + t^2\sin t}{2t^3}$$
再次应用洛必达法则:
$$= \lim _{t\rightarrow 0}\dfrac {3t\sin t + t^2\cos t}{6t^2}$$
$$= \lim _{t\rightarrow 0}\dfrac {3\sin t + t\cos t}{6t}$$
$$= \lim _{t\rightarrow 0}\dfrac {3\sin t}{6t} + \lim _{t\rightarrow 0}\dfrac {t\cos t}{6t}$$
$$= \dfrac{3}{6} + \lim _{t\rightarrow 0}\dfrac {\cos t}{6}$$
$$= \dfrac{3}{6} + \dfrac{1}{6}$$
$$= \dfrac{2}{3}$$
首先,我们观察到当$x\rightarrow \infty$时,$\dfrac{1}{x}\rightarrow 0$。因此,我们需要计算$\lim _{x\rightarrow \infty }{x}^{2}(2-x\sin \dfrac {1}{x}-\cos \dfrac {1}{x})$,这可以转换为$\lim _{t\rightarrow 0}\dfrac {1}{{t}^{2}}(2-\dfrac {1}{t}\sin t-\cos t)$,其中$t=\dfrac{1}{x}$。
步骤 2:应用洛必达法则
由于直接计算上述极限比较困难,我们应用洛必达法则。洛必达法则适用于$\dfrac{0}{0}$或$\dfrac{\infty}{\infty}$形式的极限。因此,我们有:
$$\lim _{t\rightarrow 0}\dfrac {1}{{t}^{2}}(2-\dfrac {1}{t}\sin t-\cos t) = \lim _{t\rightarrow 0}\dfrac {2-\dfrac {1}{t}\sin t-\cos t}{{t}^{2}}$$
应用洛必达法则,我们对分子和分母同时求导:
$$\lim _{t\rightarrow 0}\dfrac {2-\dfrac {1}{t}\sin t-\cos t}{{t}^{2}} = \lim _{t\rightarrow 0}\dfrac {\dfrac{d}{dt}(2-\dfrac {1}{t}\sin t-\cos t)}{\dfrac{d}{dt}({t}^{2})}$$
$$= \lim _{t\rightarrow 0}\dfrac {\dfrac{1}{t^2}\sin t - \dfrac{1}{t}\cos t + \sin t}{2t}$$
$$= \lim _{t\rightarrow 0}\dfrac {\sin t - t\cos t + t^2\sin t}{2t^3}$$
再次应用洛必达法则:
$$= \lim _{t\rightarrow 0}\dfrac {3t\sin t + t^2\cos t}{6t^2}$$
$$= \lim _{t\rightarrow 0}\dfrac {3\sin t + t\cos t}{6t}$$
$$= \lim _{t\rightarrow 0}\dfrac {3\sin t}{6t} + \lim _{t\rightarrow 0}\dfrac {t\cos t}{6t}$$
$$= \dfrac{3}{6} + \lim _{t\rightarrow 0}\dfrac {\cos t}{6}$$
$$= \dfrac{3}{6} + \dfrac{1}{6}$$
$$= \dfrac{2}{3}$$