题目
已知 f(x)= ) (x)^2,0leqslant xlt 1 1,1leqslant xleqslant 2,f(t)dt(0leqslant xleqslant 2), 则

题目解答
答案
解析:
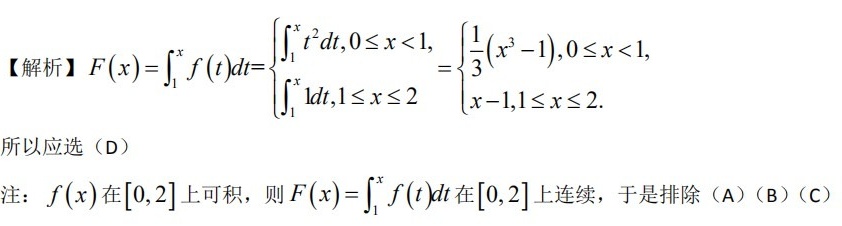
解析
步骤 1:确定积分区间
根据题目,$F(x)={\int }_{1}^{x}f(t)dt$,其中$f(x)$定义为分段函数。因此,我们需要根据$x$的取值范围来确定积分的区间。
步骤 2:计算积分
当$0\leqslant x\lt 1$时,$f(t)=t^2$,因此$F(x)={\int }_{1}^{x}t^2dt$。计算这个积分,我们得到$F(x)=\dfrac{1}{3}t^3|_{1}^{x}=\dfrac{1}{3}x^3-\dfrac{1}{3}$。
当$1\leqslant x\leqslant 2$时,$f(t)=1$,因此$F(x)={\int }_{1}^{x}1dt$。计算这个积分,我们得到$F(x)=t|_{1}^{x}=x-1$。
步骤 3:验证连续性
$f(x)$在$[0,2]$上可积,因此$F(x)$在$[0,2]$上连续。根据计算结果,$F(x)$在$x=1$处连续,因此排除(A)(B)(C)选项。
根据题目,$F(x)={\int }_{1}^{x}f(t)dt$,其中$f(x)$定义为分段函数。因此,我们需要根据$x$的取值范围来确定积分的区间。
步骤 2:计算积分
当$0\leqslant x\lt 1$时,$f(t)=t^2$,因此$F(x)={\int }_{1}^{x}t^2dt$。计算这个积分,我们得到$F(x)=\dfrac{1}{3}t^3|_{1}^{x}=\dfrac{1}{3}x^3-\dfrac{1}{3}$。
当$1\leqslant x\leqslant 2$时,$f(t)=1$,因此$F(x)={\int }_{1}^{x}1dt$。计算这个积分,我们得到$F(x)=t|_{1}^{x}=x-1$。
步骤 3:验证连续性
$f(x)$在$[0,2]$上可积,因此$F(x)$在$[0,2]$上连续。根据计算结果,$F(x)$在$x=1$处连续,因此排除(A)(B)(C)选项。