题目
求lim _(xarrow 0)dfrac ({x)^2+3x}(2{x)^2-1}.
求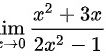 .
.
题目解答
答案
求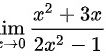 ,已知当
,已知当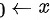 时,可得分子
时,可得分子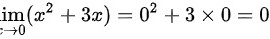 ,分母为
,分母为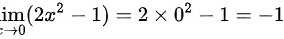 ,可得当
,可得当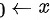 时,分母不为
时,分母不为 ,为一般的极限计算,直接将
,为一般的极限计算,直接将 代入即可,可得
代入即可,可得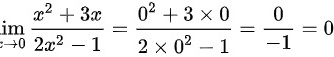 ,故
,故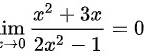 ,答案为
,答案为
解析
步骤 1:计算分子的极限
当$x\rightarrow 0$时,分子${x}^{2}+3x$的极限为$\lim _{x\rightarrow 0}({x}^{2}+3x)={0}^{2}+3\times 0=0$。
步骤 2:计算分母的极限
当$x\rightarrow 0$时,分母$2{x}^{2}-1$的极限为$\lim _{x\rightarrow 0}(2{x}^{2}-1)=2\times {0}^{2}-1=-1$。
步骤 3:计算整个表达式的极限
由于分母不为零,可以直接将$x=0$代入原表达式计算极限,即$\lim _{x\rightarrow 0}\dfrac {{x}^{2}+3x}{2{x}^{2}-1}=\dfrac {{0}^{2}+3\times 0}{2\times {0}^{2}-1}=\dfrac {0}{-1}=0$。
当$x\rightarrow 0$时,分子${x}^{2}+3x$的极限为$\lim _{x\rightarrow 0}({x}^{2}+3x)={0}^{2}+3\times 0=0$。
步骤 2:计算分母的极限
当$x\rightarrow 0$时,分母$2{x}^{2}-1$的极限为$\lim _{x\rightarrow 0}(2{x}^{2}-1)=2\times {0}^{2}-1=-1$。
步骤 3:计算整个表达式的极限
由于分母不为零,可以直接将$x=0$代入原表达式计算极限,即$\lim _{x\rightarrow 0}\dfrac {{x}^{2}+3x}{2{x}^{2}-1}=\dfrac {{0}^{2}+3\times 0}{2\times {0}^{2}-1}=\dfrac {0}{-1}=0$。