题目
=dfrac (sqrt {1+x)-sqrt (1-x)}(sqrt {1+x)+sqrt (1-x)}
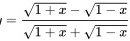
题目解答
答案
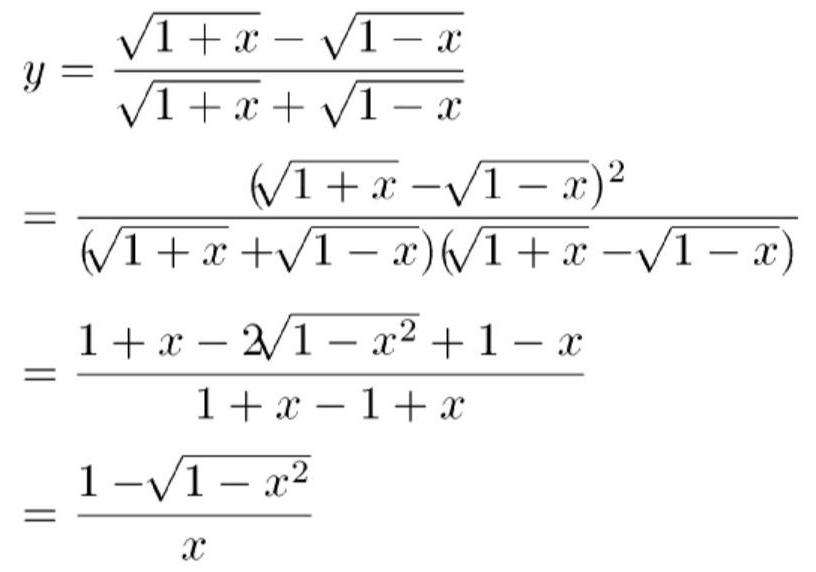
解析
步骤 1:分子分母同乘以分子的共轭表达式
为了消除分母中的根号,我们首先将分子和分母同时乘以分子的共轭表达式,即$\sqrt{1+x} - \sqrt{1-x}$。这样做的目的是利用差乘积公式$(a-b)(a+b)=a^2-b^2$来简化表达式。
步骤 2:应用差乘积公式
应用差乘积公式,分子变为$(\sqrt{1+x}-\sqrt{1-x})^2$,分母变为$(\sqrt{1+x}+\sqrt{1-x})(\sqrt{1+x}-\sqrt{1-x})$,即$1+x-(1-x)$。
步骤 3:化简表达式
分子展开为$1+x-2\sqrt{(1+x)(1-x)}+1-x$,分母简化为$2x$。进一步化简分子,得到$2-2\sqrt{1-x^2}$。
步骤 4:最终化简
将分子和分母进一步化简,得到最终的表达式。
为了消除分母中的根号,我们首先将分子和分母同时乘以分子的共轭表达式,即$\sqrt{1+x} - \sqrt{1-x}$。这样做的目的是利用差乘积公式$(a-b)(a+b)=a^2-b^2$来简化表达式。
步骤 2:应用差乘积公式
应用差乘积公式,分子变为$(\sqrt{1+x}-\sqrt{1-x})^2$,分母变为$(\sqrt{1+x}+\sqrt{1-x})(\sqrt{1+x}-\sqrt{1-x})$,即$1+x-(1-x)$。
步骤 3:化简表达式
分子展开为$1+x-2\sqrt{(1+x)(1-x)}+1-x$,分母简化为$2x$。进一步化简分子,得到$2-2\sqrt{1-x^2}$。
步骤 4:最终化简
将分子和分母进一步化简,得到最终的表达式。