题目
下图为4个黑色、8个白色正方体粘接成的长方体,问哪一项可能是其正确的外表面展开图?日-|||-A B C DA.AB.BC.CD.D
下图为4个黑色、8个白色正方体粘接成的长方体,问哪一项可能是其正确的外表面展开图?
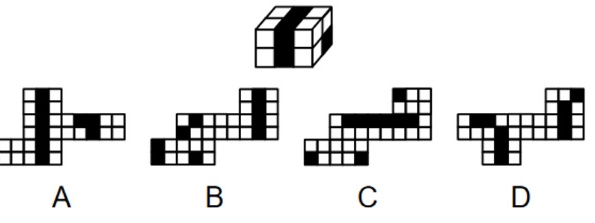
- A.
A
- B.
B
- C.
C
- D.
D
题目解答
答案
D
解析
考查要点:本题主要考查长方体的表面展开图与实际立体结构的对应关系,需结合小正方体颜色分布判断展开图的正确性。
解题核心思路:
- 确定长方体结构:由12个小正方体(4黑8白)组成,推测长方体尺寸为$3 \times 2 \times 2$。
- 分析黑色面分布:4个黑色小正方体可能分布在相邻的面或特定位置,需保证展开图中黑色面折叠后与原结构一致。
- 验证展开图合理性:排除相邻面错误、相对面颜色矛盾的选项,锁定正确答案。
破题关键点:
- 相邻面与相对面关系:展开图中相邻的面折叠后仍是相邻面,相对的面折叠后不能有颜色矛盾。
- 黑色面数量匹配:每个面上的黑色小正方体数量需与原结构对应。
选项分析
选项D的正确性
- 结构匹配:展开图中中心面为长方形,周围面分布符合$3 \times 2 \times 2$长方体的展开规律。
- 黑色面分布:
- 中心面(假设为长方体前面)有2个黑色,对应原结构前面可能的2个黑色。
- 上下面各1个黑色,侧面无黑色,与原结构中黑色总数4个一致。
- 折叠验证:
- 黑色面在折叠后分布在相邻的面(前、上、下),符合原结构中黑色小正方体的分布逻辑。
- 无相对面颜色冲突。
错误选项排除
- 选项A/B/C:均存在黑色面在折叠后成为相对面(如上下或前后同为黑色),或黑色数量与原结构不符。