题目
4.函数 =xcos x 在 (-infty ,+infty ) 内是否有界?这个函数是否为 arrow +infty 时的无穷大?
题目解答
答案
解题如下：
解：因为存在M>0，总有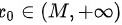
,使
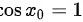，从而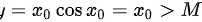
所以y=xcosx在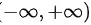
内无界
有因为存在M>0,X>0,总有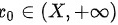
,使
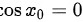,从而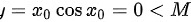
所以y=xcosx不是当
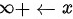时的无穷大
解析
步骤 1：判断函数是否有界
函数 $y=x\cos x$ 在 $(-\infty ,+\infty )$ 内是否有界，需要判断是否存在一个常数 $M$，使得对于所有的 $x$，都有 $|y| \leq M$。由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y=x\cos x$ 的值域为 $[-x,x]$。随着 $x$ 的增大，$y$ 的值域也会增大，因此不存在一个常数 $M$ 使得 $|y| \leq M$ 对于所有的 $x$ 都成立。所以，函数 $y=x\cos x$ 在 $(-\infty ,+\infty )$ 内无界。
步骤 2：判断函数是否为 $x\rightarrow +\infty $ 时的无穷大
函数 $y=x\cos x$ 是否为 $x\rightarrow +\infty $ 时的无穷大，需要判断是否存在一个常数 $M$，使得对于所有的 $x$，当 $x>M$ 时，都有 $|y| > M$。由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y=x\cos x$ 的值域为 $[-x,x]$。随着 $x$ 的增大，$y$ 的值域也会增大，但是由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y$ 的值域不会一直增大，而是会在 $[-x,x]$ 之间波动。因此，不存在一个常数 $M$ 使得 $|y| > M$ 对于所有的 $x$ 都成立。所以，函数 $y=x\cos x$ 不是 $x\rightarrow +\infty $ 时的无穷大。
函数 $y=x\cos x$ 在 $(-\infty ,+\infty )$ 内是否有界，需要判断是否存在一个常数 $M$，使得对于所有的 $x$，都有 $|y| \leq M$。由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y=x\cos x$ 的值域为 $[-x,x]$。随着 $x$ 的增大，$y$ 的值域也会增大，因此不存在一个常数 $M$ 使得 $|y| \leq M$ 对于所有的 $x$ 都成立。所以，函数 $y=x\cos x$ 在 $(-\infty ,+\infty )$ 内无界。
步骤 2：判断函数是否为 $x\rightarrow +\infty $ 时的无穷大
函数 $y=x\cos x$ 是否为 $x\rightarrow +\infty $ 时的无穷大，需要判断是否存在一个常数 $M$，使得对于所有的 $x$，当 $x>M$ 时，都有 $|y| > M$。由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y=x\cos x$ 的值域为 $[-x,x]$。随着 $x$ 的增大，$y$ 的值域也会增大，但是由于 $\cos x$ 的值域为 $[-1,1]$，因此 $y$ 的值域不会一直增大，而是会在 $[-x,x]$ 之间波动。因此，不存在一个常数 $M$ 使得 $|y| > M$ 对于所有的 $x$ 都成立。所以，函数 $y=x\cos x$ 不是 $x\rightarrow +\infty $ 时的无穷大。