学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题 在曲线学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题上一点学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题处作切线,该曲线、切线与学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题轴围成图形学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题的面积为学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题,求切点坐标和切线方程,并求图形学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题绕学号-|||-班级-|||-姓名 装-|||-订-|||-装-|||-线-|||-订-|||-线-|||-内-|||-不-|||-要-|||-答-|||-题轴旋转一周所得的旋转体的体积。
 在曲线
在曲线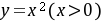 上一点
上一点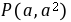 处作切线,该曲线、切线与
处作切线,该曲线、切线与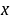 轴围成图形
轴围成图形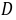 的面积为
的面积为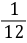 ,求切点坐标和切线方程,并求图形
,求切点坐标和切线方程,并求图形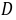 绕
绕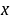 轴旋转一周所得的旋转体的体积。
轴旋转一周所得的旋转体的体积。
题目解答
答案
解: 切线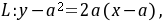 即
即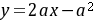 。
。
令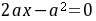 ,得切线与
,得切线与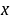 轴交点坐标为
轴交点坐标为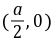 。(2分)
。(2分)
由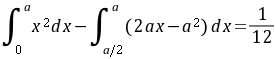 解得
解得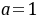 ,故切点坐标为
,故切点坐标为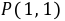 ,切线方程为
,切线方程为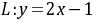 。(4分)
。(4分)
体积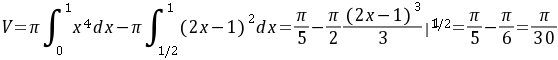 。(8分)
。(8分)
解析
考查要点:本题综合考查导数的几何意义(求切线方程)、定积分计算平面图形面积、以及旋转体体积的计算方法。
解题思路:
- 求切线方程:利用导数求出切线斜率,写出点斜式方程。
- 确定积分区间:分析曲线、切线与x轴的交点,明确所求面积的构成区域。
- 列方程求参数:通过积分计算面积,建立方程解出参数$a$。
- 计算旋转体体积:应用圆盘法分段积分,求出绕x轴旋转的体积。
破题关键:
- 切线方程的正确性:导数计算准确,方程整理无误。
- 积分区间的划分:正确识别图形由抛物线、切线、x轴围成的两部分区域。
- 体积计算的分段处理:区分内外函数,正确应用圆盘法公式。
求切线方程
曲线$y = x^2$在点$P(a, a^2)$处的导数为$y' = 2x$,故切线斜率为$2a$。
切线方程为:
$y - a^2 = 2a(x - a) \implies y = 2ax - a^2.$
求切线与x轴的交点
令$y = 0$,解得:
$2ax - a^2 = 0 \implies x = \frac{a}{2}.$
交点为$\left(\frac{a}{2}, 0\right)$。
计算面积并解方程
图形由抛物线$y = x^2$、切线$y = 2ax - a^2$和x轴围成,分为两部分:
- 从$x = 0$到$x = \frac{a}{2}$:面积为抛物线下方面积;
- 从$x = \frac{a}{2}$到$x = a$:面积为抛物线与切线之间的面积。
总面积方程为:
$\int_{0}^{a} x^2 \, dx - \int_{\frac{a}{2}}^{a} (2ax - a^2) \, dx = \frac{1}{12}.$
计算积分:
- $\int_{0}^{a} x^2 \, dx = \frac{a^3}{3}$;
- $\int_{\frac{a}{2}}^{a} (2ax - a^2) \, dx = \frac{a^3}{4}$。
代入方程:
$\frac{a^3}{3} - \frac{a^3}{4} = \frac{1}{12} \implies \frac{a^3}{12} = \frac{1}{12} \implies a = 1.$
求体积
图形绕x轴旋转,体积分为两部分:
- 从$x = 0$到$x = \frac{1}{2}$:外半径为$x^2$,内半径为$0$;
- 从$x = \frac{1}{2}$到$x = 1$:外半径为$x^2$,内半径为$2x - 1$。
体积公式为:
$V = \pi \left( \int_{0}^{\frac{1}{2}} (x^2)^2 \, dx + \int_{\frac{1}{2}}^{1} \left[(x^2)^2 - (2x - 1)^2\right] \, dx \right).$
计算积分:
- $\int_{0}^{\frac{1}{2}} x^4 \, dx = \frac{1}{160}$;
- $\int_{\frac{1}{2}}^{1} \left(x^4 - (4x^2 - 4x + 1)\right) \, dx = \frac{13}{480}$。
总体积:
$V = \pi \left( \frac{1}{160} + \frac{13}{480} \right) = \frac{\pi}{30}.$