题目
8.设函数f(x)在点 x=1 处连续,且 lim _(xarrow 1)dfrac (f(x)-2)(x-1) 存在,则 f(1)= __
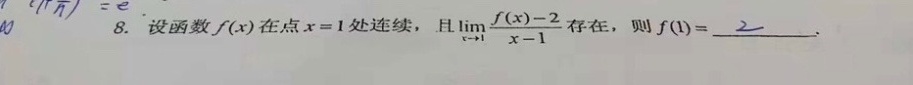
题目解答
答案

解析
步骤 1:理解题意
题目给出函数f(x)在点x=1处连续,且$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1}$存在。这意味着f(x)在x=1处的导数存在,且f(x)在x=1处的值是确定的。
步骤 2:利用极限的性质
由于$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1}$存在,设其值为L,则有$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1} = L$。根据极限的定义,当x趋近于1时,$\dfrac {f(x)-2}{x-1}$的值趋近于L。
步骤 3:求f(1)的值
由于f(x)在x=1处连续,根据连续函数的定义,$\lim _{x\rightarrow 1}f(x) = f(1)$。同时,根据步骤2中的极限表达式,当x趋近于1时,$f(x)-2$的值趋近于0,即$\lim _{x\rightarrow 1}f(x) = 2$。因此,f(1) = 2。
题目给出函数f(x)在点x=1处连续,且$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1}$存在。这意味着f(x)在x=1处的导数存在,且f(x)在x=1处的值是确定的。
步骤 2:利用极限的性质
由于$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1}$存在,设其值为L,则有$\lim _{x\rightarrow 1}\dfrac {f(x)-2}{x-1} = L$。根据极限的定义,当x趋近于1时,$\dfrac {f(x)-2}{x-1}$的值趋近于L。
步骤 3:求f(1)的值
由于f(x)在x=1处连续,根据连续函数的定义,$\lim _{x\rightarrow 1}f(x) = f(1)$。同时,根据步骤2中的极限表达式,当x趋近于1时,$f(x)-2$的值趋近于0,即$\lim _{x\rightarrow 1}f(x) = 2$。因此,f(1) = 2。