题目
求(x,y)=((x-1))^2+((y-2))^2+1在区域(x,y)=((x-1))^2+((y-2))^2+1上的最大值和最小值.
求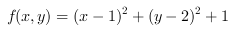
在区域
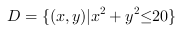上的最大值和最小值.
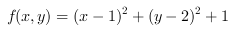在区域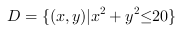上的最大值和最小值.题目解答
答案
解析
步骤 1：确定函数$f(x,y)$的几何意义
函数$f(x,y)={(x-1)}^{2}+{(y-2)}^{2}+1$表示点$(x,y)$到点$(1,2)$的距离的平方加上1。因此，$f(x,y)$的值与点$(x,y)$到点$(1,2)$的距离有关。
步骤 2：确定区域$D$的几何意义
区域$D=\{ (x,y)|{x}^{2}+{y}^{2}\leqslant 20\}$表示以原点$(0,0)$为圆心，半径为$\sqrt{20}$的圆及其内部的所有点。
步骤 3：确定$f(x,y)$在区域$D$上的最大值和最小值
由于$f(x,y)$表示点$(x,y)$到点$(1,2)$的距离的平方加上1，因此$f(x,y)$的值在区域$D$上的最大值和最小值分别对应于点$(x,y)$到点$(1,2)$的距离的最大值和最小值。点$(1,2)$到圆心$(0,0)$的距离为$\sqrt{1^2+2^2}=\sqrt{5}$，因此点$(x,y)$到点$(1,2)$的距离的最大值为$\sqrt{20}+\sqrt{5}$，最小值为$\sqrt{20}-\sqrt{5}$。因此，$f(x,y)$的最大值为$(\sqrt{20}+\sqrt{5})^2+1=20+2\sqrt{100}+5+1=26+20=46$，最小值为$(\sqrt{20}-\sqrt{5})^2+1=20-2\sqrt{100}+5+1=26-20=1$。
函数$f(x,y)={(x-1)}^{2}+{(y-2)}^{2}+1$表示点$(x,y)$到点$(1,2)$的距离的平方加上1。因此，$f(x,y)$的值与点$(x,y)$到点$(1,2)$的距离有关。
步骤 2：确定区域$D$的几何意义
区域$D=\{ (x,y)|{x}^{2}+{y}^{2}\leqslant 20\}$表示以原点$(0,0)$为圆心，半径为$\sqrt{20}$的圆及其内部的所有点。
步骤 3：确定$f(x,y)$在区域$D$上的最大值和最小值
由于$f(x,y)$表示点$(x,y)$到点$(1,2)$的距离的平方加上1，因此$f(x,y)$的值在区域$D$上的最大值和最小值分别对应于点$(x,y)$到点$(1,2)$的距离的最大值和最小值。点$(1,2)$到圆心$(0,0)$的距离为$\sqrt{1^2+2^2}=\sqrt{5}$，因此点$(x,y)$到点$(1,2)$的距离的最大值为$\sqrt{20}+\sqrt{5}$，最小值为$\sqrt{20}-\sqrt{5}$。因此，$f(x,y)$的最大值为$(\sqrt{20}+\sqrt{5})^2+1=20+2\sqrt{100}+5+1=26+20=46$，最小值为$(\sqrt{20}-\sqrt{5})^2+1=20-2\sqrt{100}+5+1=26-20=1$。