题目
已知实数a≠0,求函数(x)=(a)^2(x)^3-6a(x)^2+9x-|||-__的极值,并判断是极大值还是极小值。
已知实数a≠0,求函数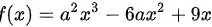 的极值,并判断是极大值还是极小值。
的极值,并判断是极大值还是极小值。
题目解答
答案
已知函数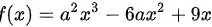
则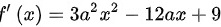
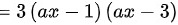
令一阶导数等于0,得到驻点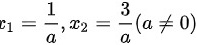
再求出二阶导数为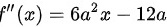
所以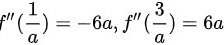
当a<0时,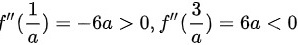 ,所以驻点
,所以驻点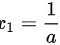 为极小值,驻点
为极小值,驻点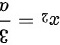 为极大值
为极大值
当a>0时,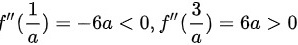 ,所以驻点
,所以驻点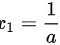 为极大值,驻点
为极大值,驻点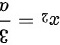 为极小值
为极小值
解析
步骤 1:求一阶导数
对函数$f(x)={a}^{2}{x}^{3}-6a{x}^{2}+9x$求一阶导数,得到$f'(x)=3{a}^{2}{x}^{2}-12ax+9$。
步骤 2:求驻点
令一阶导数等于0,即$3{a}^{2}{x}^{2}-12ax+9=0$,解得驻点${c}_{1}=\dfrac {1}{a}$和${x}_{2}=\dfrac {3}{a}$。
步骤 3:求二阶导数
对一阶导数求导,得到二阶导数$f''(x)=6{a}^{2}x-12a$。
步骤 4:判断极值
将驻点代入二阶导数中,得到$f''(\dfrac {1}{a})=-6a$和$f''(\dfrac {3}{a})=6a$。当$a<0$时,$f''(\dfrac {1}{a})>0$,$f''(\dfrac {3}{a})<0$,所以${c}_{1}=\dfrac {1}{a}$为极小值,${x}_{2}=\dfrac {3}{a}$为极大值。当$a>0$时,$f''(\dfrac {1}{a})<0$,$f''(\dfrac {3}{a})>0$,所以${c}_{1}=\dfrac {1}{a}$为极大值,${x}_{2}=\dfrac {3}{a}$为极小值。
对函数$f(x)={a}^{2}{x}^{3}-6a{x}^{2}+9x$求一阶导数,得到$f'(x)=3{a}^{2}{x}^{2}-12ax+9$。
步骤 2:求驻点
令一阶导数等于0,即$3{a}^{2}{x}^{2}-12ax+9=0$,解得驻点${c}_{1}=\dfrac {1}{a}$和${x}_{2}=\dfrac {3}{a}$。
步骤 3:求二阶导数
对一阶导数求导,得到二阶导数$f''(x)=6{a}^{2}x-12a$。
步骤 4:判断极值
将驻点代入二阶导数中,得到$f''(\dfrac {1}{a})=-6a$和$f''(\dfrac {3}{a})=6a$。当$a<0$时,$f''(\dfrac {1}{a})>0$,$f''(\dfrac {3}{a})<0$,所以${c}_{1}=\dfrac {1}{a}$为极小值,${x}_{2}=\dfrac {3}{a}$为极大值。当$a>0$时,$f''(\dfrac {1}{a})<0$,$f''(\dfrac {3}{a})>0$,所以${c}_{1}=\dfrac {1}{a}$为极大值,${x}_{2}=\dfrac {3}{a}$为极小值。