证明:lim _(narrow infty )(({2)^n+(4)^n+(6)^n)}^dfrac (1{n)}=6.
证明: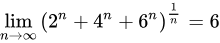 .
.
题目解答
答案
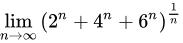
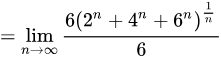
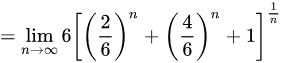
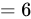
解析
考查要点:本题主要考查数列极限的计算,特别是处理形如$(a^n + b^n + c^n)^{1/n}$的极限问题。关键在于识别主导项并利用其性质简化表达式。
解题核心思路:
当$n$趋向于无穷大时,若$a < b < c$,则$c^n$会主导整个和$a^n + b^n + c^n$。因此,可以将最大项$c^n$提取出来,转化为$c \cdot \left(1 + \left(\frac{a}{c}\right)^n + \left(\frac{b}{c}\right)^n\right)^{1/n}$,再利用$\lim_{n \to \infty} \left(\frac{a}{c}\right)^n = 0$(当$a < c$时)求解。
破题关键点:
- 提取最大项:将$6^n$作为主导项提取出来。
- 分析剩余项的极限:剩余项$\left(\frac{2}{6}\right)^n$和$\left(\frac{4}{6}\right)^n$均趋向于0,从而整体趋向于1。
- 结合幂运算性质:利用$\lim_{n \to \infty} 1^{1/n} = 1$得出最终结果。
步骤1:提取主导项
将原式中的$6^n$提取出来:
$\begin{aligned}\lim_{n \to \infty} (2^n + 4^n + 6^n)^{1/n} &= \lim_{n \to \infty} \left[6^n \left(\left(\frac{2}{6}\right)^n + \left(\frac{4}{6}\right)^n + 1\right)\right]^{1/n} \\&= \lim_{n \to \infty} 6 \cdot \left[\left(\frac{1}{3}\right)^n + \left(\frac{2}{3}\right)^n + 1\right]^{1/n}.\end{aligned}$
步骤2:分析剩余项的极限
当$n \to \infty$时,$\left(\frac{1}{3}\right)^n \to 0$,$\left(\frac{2}{3}\right)^n \to 0$,因此:
$\left(\frac{1}{3}\right)^n + \left(\frac{2}{3}\right)^n + 1 \to 0 + 0 + 1 = 1.$
步骤3:结合幂运算性质
由于$\lim_{n \to \infty} 1^{1/n} = 1$,故:
$\lim_{n \to \infty} 6 \cdot \left[\left(\frac{1}{3}\right)^n + \left(\frac{2}{3}\right)^n + 1\right]^{1/n} = 6 \cdot 1 = 6.$