题目
(5) lim _(xarrow 1)dfrac (sqrt {5x-4)-sqrt (x)}(x-1);
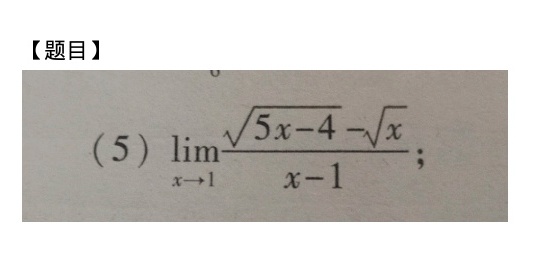
题目解答
答案

解析
步骤 1:有理化分子
为了消除根号,我们可以通过乘以分子和分母的共轭来有理化分子。分子的共轭是 $\sqrt{5x-4} + \sqrt{x}$。因此,我们有:
$$\lim _{x\rightarrow 1}\dfrac {\sqrt {5x-4}-\sqrt {x}}{x-1} = \lim _{x\rightarrow 1}\dfrac {(\sqrt {5x-4}-\sqrt {x})(\sqrt {5x-4}+\sqrt {x})}{(x-1)(\sqrt {5x-4}+\sqrt {x})}$$
步骤 2:简化表达式
分子可以简化为 $(5x-4) - x = 4x - 4$,因此:
$$\lim _{x\rightarrow 1}\dfrac {4x-4}{(x-1)(\sqrt {5x-4}+\sqrt {x})}$$
步骤 3:进一步简化
由于 $4x - 4 = 4(x - 1)$,我们可以进一步简化表达式:
$$\lim _{x\rightarrow 1}\dfrac {4(x-1)}{(x-1)(\sqrt {5x-4}+\sqrt {x})} = \lim _{x\rightarrow 1}\dfrac {4}{\sqrt {5x-4}+\sqrt {x}}$$
步骤 4:计算极限
将 $x = 1$ 代入表达式中,得到:
$$\lim _{x\rightarrow 1}\dfrac {4}{\sqrt {5x-4}+\sqrt {x}} = \dfrac {4}{\sqrt {5(1)-4}+\sqrt {1}} = \dfrac {4}{\sqrt {1}+\sqrt {1}} = \dfrac {4}{2} = 2$$
为了消除根号,我们可以通过乘以分子和分母的共轭来有理化分子。分子的共轭是 $\sqrt{5x-4} + \sqrt{x}$。因此,我们有:
$$\lim _{x\rightarrow 1}\dfrac {\sqrt {5x-4}-\sqrt {x}}{x-1} = \lim _{x\rightarrow 1}\dfrac {(\sqrt {5x-4}-\sqrt {x})(\sqrt {5x-4}+\sqrt {x})}{(x-1)(\sqrt {5x-4}+\sqrt {x})}$$
步骤 2:简化表达式
分子可以简化为 $(5x-4) - x = 4x - 4$,因此:
$$\lim _{x\rightarrow 1}\dfrac {4x-4}{(x-1)(\sqrt {5x-4}+\sqrt {x})}$$
步骤 3:进一步简化
由于 $4x - 4 = 4(x - 1)$,我们可以进一步简化表达式:
$$\lim _{x\rightarrow 1}\dfrac {4(x-1)}{(x-1)(\sqrt {5x-4}+\sqrt {x})} = \lim _{x\rightarrow 1}\dfrac {4}{\sqrt {5x-4}+\sqrt {x}}$$
步骤 4:计算极限
将 $x = 1$ 代入表达式中,得到:
$$\lim _{x\rightarrow 1}\dfrac {4}{\sqrt {5x-4}+\sqrt {x}} = \dfrac {4}{\sqrt {5(1)-4}+\sqrt {1}} = \dfrac {4}{\sqrt {1}+\sqrt {1}} = \dfrac {4}{2} = 2$$