题目
计算__-|||-lim _(xarrow infty )((sin dfrac {1)(x)+cos dfrac (1)(x))}^x
计算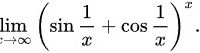
题目解答
答案
已知重要极限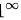 型极限:
型极限:
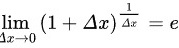
将题目极限进行变形
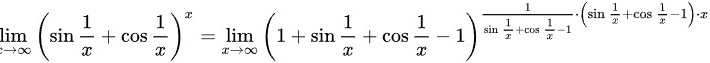
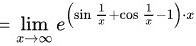
故转变成求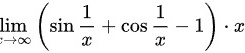
我们可以使用倒代换
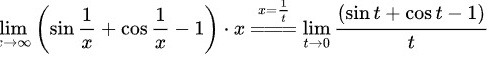
使用洛必达法则
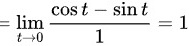
故
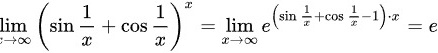
解析
步骤 1:使用重要极限
已知重要极限:$\lim _{\Delta x\rightarrow 0}{(1+\Delta x)}^{\dfrac {1}{\Delta x}}=e$。将题目中的极限进行变形,以便使用这个重要极限。
步骤 2:变形极限
将题目中的极限变形为:$\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}=\lim _{x\rightarrow \infty }{e}^{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x}$。
步骤 3:求解指数部分的极限
求解$\lim _{x\rightarrow \infty }(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x$。使用倒代换$t=\dfrac {1}{x}$,则$x=\dfrac {1}{t}$,当$x\rightarrow \infty$时,$t\rightarrow 0$。因此,原极限变为$\lim _{t\rightarrow 0}\dfrac {\sin t+\cos t-1}{t}$。
步骤 4:使用洛必达法则
使用洛必达法则求解$\lim _{t\rightarrow 0}\dfrac {\sin t+\cos t-1}{t}$。对分子和分母分别求导,得到$\lim _{t\rightarrow 0}\dfrac {\cos t-\sin t}{1}$。
步骤 5:计算极限值
计算$\lim _{t\rightarrow 0}\dfrac {\cos t-\sin t}{1}=\dfrac {\cos 0-\sin 0}{1}=1$。
步骤 6:得出最终结果
将步骤 5 的结果代入步骤 2 的变形极限中,得到$\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}=\lim _{x\rightarrow \infty }{e}^{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x}=e^{1}=e$。
已知重要极限:$\lim _{\Delta x\rightarrow 0}{(1+\Delta x)}^{\dfrac {1}{\Delta x}}=e$。将题目中的极限进行变形,以便使用这个重要极限。
步骤 2:变形极限
将题目中的极限变形为:$\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}=\lim _{x\rightarrow \infty }{e}^{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x}$。
步骤 3:求解指数部分的极限
求解$\lim _{x\rightarrow \infty }(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x$。使用倒代换$t=\dfrac {1}{x}$,则$x=\dfrac {1}{t}$,当$x\rightarrow \infty$时,$t\rightarrow 0$。因此,原极限变为$\lim _{t\rightarrow 0}\dfrac {\sin t+\cos t-1}{t}$。
步骤 4:使用洛必达法则
使用洛必达法则求解$\lim _{t\rightarrow 0}\dfrac {\sin t+\cos t-1}{t}$。对分子和分母分别求导,得到$\lim _{t\rightarrow 0}\dfrac {\cos t-\sin t}{1}$。
步骤 5:计算极限值
计算$\lim _{t\rightarrow 0}\dfrac {\cos t-\sin t}{1}=\dfrac {\cos 0-\sin 0}{1}=1$。
步骤 6:得出最终结果
将步骤 5 的结果代入步骤 2 的变形极限中,得到$\lim _{x\rightarrow \infty }{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x})}^{x}=\lim _{x\rightarrow \infty }{e}^{(\sin \dfrac {1}{x}+\cos \dfrac {1}{x}-1)\cdot x}=e^{1}=e$。