题目
int dfrac (1)(1+cos 2x)dx=______.
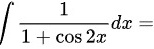 ______.
______.
题目解答
答案
∵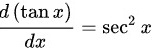
∴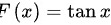 是
是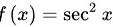 的一个原函数
的一个原函数
∴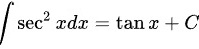 ,则
,则
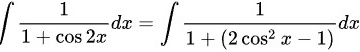
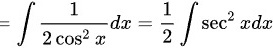
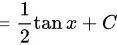
解析
步骤 1:利用二倍角公式
将$\cos 2x$用二倍角公式表示,即$\cos 2x = 2\cos^2 x - 1$。
步骤 2:化简积分表达式
将$\cos 2x$的表达式代入原积分表达式中,得到$\int \dfrac {1}{1+(2\cos^2 x - 1)}dx$,化简后得到$\int \dfrac {1}{2\cos^2 x}dx$。
步骤 3:利用三角恒等式
利用三角恒等式${\sec}^2 x = \dfrac{1}{\cos^2 x}$,将积分表达式进一步化简为$\dfrac{1}{2}\int {\sec}^2 x dx$。
步骤 4:求解积分
根据积分公式$\int {\sec}^2 x dx = \tan x + C$,求解得到$\dfrac{1}{2}\tan x + C$。
将$\cos 2x$用二倍角公式表示,即$\cos 2x = 2\cos^2 x - 1$。
步骤 2:化简积分表达式
将$\cos 2x$的表达式代入原积分表达式中,得到$\int \dfrac {1}{1+(2\cos^2 x - 1)}dx$,化简后得到$\int \dfrac {1}{2\cos^2 x}dx$。
步骤 3:利用三角恒等式
利用三角恒等式${\sec}^2 x = \dfrac{1}{\cos^2 x}$,将积分表达式进一步化简为$\dfrac{1}{2}\int {\sec}^2 x dx$。
步骤 4:求解积分
根据积分公式$\int {\sec}^2 x dx = \tan x + C$,求解得到$\dfrac{1}{2}\tan x + C$。