题目
lim _(xarrow 0)((1+x))^dfrac (3{x)}=;
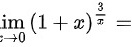 ;
;
题目解答
答案
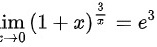
即为本题答案。
解析
步骤 1:识别极限形式
给定的极限形式为 $\lim _{x\rightarrow 0}{(1+x)}^{\dfrac {3}{x}}$,这是一个典型的指数函数的极限形式,其中底数为 $(1+x)$,指数为 $\dfrac{3}{x}$。当 $x$ 趋近于 $0$ 时,底数 $(1+x)$ 趋近于 $1$,而指数 $\dfrac{3}{x}$ 趋向于无穷大,这符合 $1^\infty$ 的不定型。
步骤 2:转换为自然对数形式
为了处理这种不定型,我们可以将原极限转换为自然对数形式。设 $y = {(1+x)}^{\dfrac {3}{x}}$,则有 $\ln y = \dfrac{3}{x} \ln(1+x)$。现在,我们求 $\lim _{x\rightarrow 0} \ln y$,即 $\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x)$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x)$ 是 $\dfrac{0}{0}$ 的不定型,我们可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a} \dfrac{f(x)}{g(x)}$ 是 $\dfrac{0}{0}$ 或 $\dfrac{\infty}{\infty}$ 的不定型,那么 $\lim _{x\rightarrow a} \dfrac{f(x)}{g(x)} = \lim _{x\rightarrow a} \dfrac{f'(x)}{g'(x)}$,如果后者存在或为无穷大。因此,我们有
$$\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x) = \lim _{x\rightarrow 0} \dfrac{3 \cdot \dfrac{1}{1+x}}{1} = \lim _{x\rightarrow 0} \dfrac{3}{1+x} = 3$$
步骤 4:求解原极限
由于 $\ln y$ 的极限为 $3$,则 $y$ 的极限为 $e^3$。因此,原极限 $\lim _{x\rightarrow 0}{(1+x)}^{\dfrac {3}{x}} = e^3$。
给定的极限形式为 $\lim _{x\rightarrow 0}{(1+x)}^{\dfrac {3}{x}}$,这是一个典型的指数函数的极限形式,其中底数为 $(1+x)$,指数为 $\dfrac{3}{x}$。当 $x$ 趋近于 $0$ 时,底数 $(1+x)$ 趋近于 $1$,而指数 $\dfrac{3}{x}$ 趋向于无穷大,这符合 $1^\infty$ 的不定型。
步骤 2:转换为自然对数形式
为了处理这种不定型,我们可以将原极限转换为自然对数形式。设 $y = {(1+x)}^{\dfrac {3}{x}}$,则有 $\ln y = \dfrac{3}{x} \ln(1+x)$。现在,我们求 $\lim _{x\rightarrow 0} \ln y$,即 $\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x)$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x)$ 是 $\dfrac{0}{0}$ 的不定型,我们可以应用洛必达法则。洛必达法则指出,如果 $\lim _{x\rightarrow a} \dfrac{f(x)}{g(x)}$ 是 $\dfrac{0}{0}$ 或 $\dfrac{\infty}{\infty}$ 的不定型,那么 $\lim _{x\rightarrow a} \dfrac{f(x)}{g(x)} = \lim _{x\rightarrow a} \dfrac{f'(x)}{g'(x)}$,如果后者存在或为无穷大。因此,我们有
$$\lim _{x\rightarrow 0} \dfrac{3}{x} \ln(1+x) = \lim _{x\rightarrow 0} \dfrac{3 \cdot \dfrac{1}{1+x}}{1} = \lim _{x\rightarrow 0} \dfrac{3}{1+x} = 3$$
步骤 4:求解原极限
由于 $\ln y$ 的极限为 $3$,则 $y$ 的极限为 $e^3$。因此,原极限 $\lim _{x\rightarrow 0}{(1+x)}^{\dfrac {3}{x}} = e^3$。