题目
[题目]设函数-|||-f(x)= ) (x)^2,xleqslant 1 ax+b,xgt 1 . 在 x=1 处-|||-可导,求a,b的值。
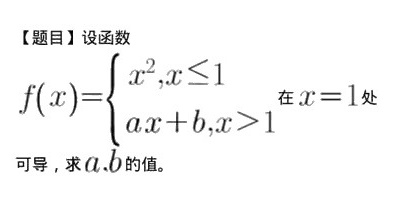
题目解答
答案
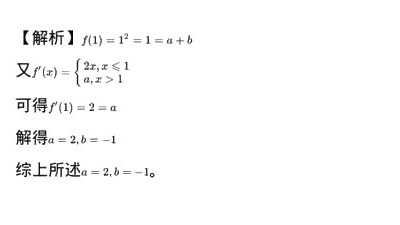
解析
步骤 1:确定函数在 x=1 处的连续性
函数 f(x) 在 x=1 处可导,首先需要保证它在该点连续。这意味着函数在 x=1 处的左极限和右极限必须相等,且等于函数在该点的值。因此,我们有:
$$
\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1)
$$
对于 x ≤ 1,f(x) = x^2,所以 f(1) = 1^2 = 1。对于 x > 1,f(x) = ax + b,所以右极限为 a*1 + b = a + b。因此,我们得到:
$$
1 = a + b
$$
步骤 2:确定函数在 x=1 处的可导性
函数 f(x) 在 x=1 处可导,意味着它的左导数和右导数必须相等。对于 x ≤ 1,f(x) = x^2,所以 f'(x) = 2x,因此左导数为 2*1 = 2。对于 x > 1,f(x) = ax + b,所以 f'(x) = a,因此右导数为 a。因此,我们得到:
$$
2 = a
$$
步骤 3:求解 a 和 b 的值
根据步骤 1 和步骤 2,我们得到两个方程:
$$
1 = a + b
$$
$$
2 = a
$$
将 a = 2 代入第一个方程,得到:
$$
1 = 2 + b
$$
解得:
$$
b = -1
$$
函数 f(x) 在 x=1 处可导,首先需要保证它在该点连续。这意味着函数在 x=1 处的左极限和右极限必须相等,且等于函数在该点的值。因此,我们有:
$$
\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1)
$$
对于 x ≤ 1,f(x) = x^2,所以 f(1) = 1^2 = 1。对于 x > 1,f(x) = ax + b,所以右极限为 a*1 + b = a + b。因此,我们得到:
$$
1 = a + b
$$
步骤 2:确定函数在 x=1 处的可导性
函数 f(x) 在 x=1 处可导,意味着它的左导数和右导数必须相等。对于 x ≤ 1,f(x) = x^2,所以 f'(x) = 2x,因此左导数为 2*1 = 2。对于 x > 1,f(x) = ax + b,所以 f'(x) = a,因此右导数为 a。因此,我们得到:
$$
2 = a
$$
步骤 3:求解 a 和 b 的值
根据步骤 1 和步骤 2,我们得到两个方程:
$$
1 = a + b
$$
$$
2 = a
$$
将 a = 2 代入第一个方程,得到:
$$
1 = 2 + b
$$
解得:
$$
b = -1
$$