题目
设有向量组_(1)=((-1,2,1))^T (beta )_(2)=((1,0,b))^7可由向量组 _(1)=((-1,2,1))^T (beta )_(2)=((1,0,b))^7线性表示. ( 1 ) 求 _(1)=((-1,2,1))^T (beta )_(2)=((1,0,b))^7的值 ; ( 2 ) 写出_(1)=((-1,2,1))^T (beta )_(2)=((1,0,b))^7 由 _(1)=((-1,2,1))^T (beta )_(2)=((1,0,b))^7 表示的线性表示式.
设有向量组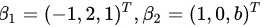 可由向量组
可由向量组 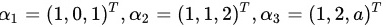 线性表示.
线性表示.
( 1 ) 求 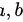 的值 ;
的值 ;
( 2 ) 写出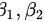 由
由 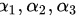 表示的线性表示式.
表示的线性表示式.
题目解答
答案
(1) 根据题目已知条件,可列出如下线性表示方程组:
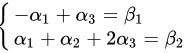
将向量表达式代入方程组,化简得到如下等式:
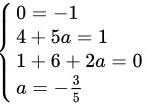 .解得
.解得 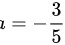 。代入第二个方程中,得到:
。代入第二个方程中,得到: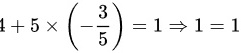
这个等式恒成立。
(2) 根据线性表示的定义,我们要找到一组系数使得线性组合等于相应的向量。设系数为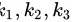 ,代入线性表示关系,得到方程组:
,代入线性表示关系,得到方程组:
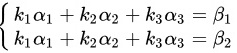
代入向量表达式,化简得到如下等式:
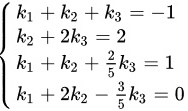 ,解得:
,解得:
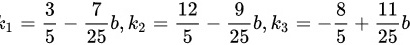
将 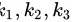 代入线性表示关系,得到线性表示式为:
代入线性表示关系,得到线性表示式为:
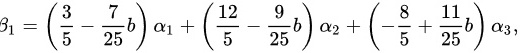
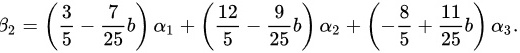
解析
步骤 1:确定向量组的线性表示关系
根据题目已知条件,向量组 ${\beta }_{1}$ 和 ${\beta }_{2}$ 可以由向量组 ${\alpha }_{1}$, ${\alpha }_{2}$, ${\alpha }_{3}$ 线性表示。这意味着存在一组系数使得线性组合等于相应的向量。设系数为 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$,代入线性表示关系,得到方程组:
$\left \{ \begin{matrix} -{\alpha }_{1}+{\alpha }_{3}={\beta }_{1}\\ {\alpha }_{1}+{\alpha }_{2}+2{\alpha }_{3}={\beta }_{2}\end{matrix} \right.$
步骤 2:代入向量表达式,化简得到等式
将向量表达式代入方程组,化简得到如下等式:
$\left \{ \begin{matrix} 0=-1\\ 4+5a=1\\ 1+6+2a=0\\ a=-\dfrac {3}{5}\end{matrix} \right.$
解得 $a=-\dfrac {3}{5}$。代入第二个方程中,得到:$4+5\times (-\dfrac {3}{5})=1\Longrightarrow 1=1=1$
这个等式恒成立。
步骤 3:求解线性表示式
根据线性表示的定义,我们要找到一组系数使得线性组合等于相应的向量。设系数为 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$,代入线性表示关系,得到方程组:
$\int {k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}+{k}_{3}{\alpha }_{3}=$ ${k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}+{k}_{3}{\alpha }_{3}=$
代入向量表达式,化简得到如下等式:
$\left \{ \begin{matrix} {k}_{1}+{k}_{2}+{k}_{3}=-1\\ {k}_{2}+2{k}_{3}=2\\ {k}_{1}+{k}_{2}+\dfrac {2}{5}{k}_{3}=1\\ {k}_{1}+2{k}_{2}-\dfrac { \right.$,解得:
${k}_{1}=\dfrac {3}{5}-\dfrac {7}{25}b$ ${k}_{2}=\dfrac {12}{5}-\dfrac {9}{25}b$ ${k}_{3}=-\dfrac {8}{5}+\dfrac {11}{25}b$
将 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$ 代入线性表示关系,得到线性表示式为:
${\beta }_{1}=\left(\dfrac {3}{5}-\dfrac {7}{25}b\right){\alpha }_{1}+\left(\dfrac {12}{5}-\dfrac {9}{25}b\right){\alpha }_{2}+\left(-\dfrac {8}{5}+\dfrac {11}{25}b\right){\alpha }_{3}$
${\beta }_{2}=\left(\dfrac {3}{5}-\dfrac {7}{25}b\right){\alpha }_{1}+\left(\dfrac {12}{5}-\dfrac {9}{25}b\right){\alpha }_{2}+\left(-\dfrac {8}{5}+\dfrac {11}{25}b\right){\alpha }_{3}$
根据题目已知条件,向量组 ${\beta }_{1}$ 和 ${\beta }_{2}$ 可以由向量组 ${\alpha }_{1}$, ${\alpha }_{2}$, ${\alpha }_{3}$ 线性表示。这意味着存在一组系数使得线性组合等于相应的向量。设系数为 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$,代入线性表示关系,得到方程组:
$\left \{ \begin{matrix} -{\alpha }_{1}+{\alpha }_{3}={\beta }_{1}\\ {\alpha }_{1}+{\alpha }_{2}+2{\alpha }_{3}={\beta }_{2}\end{matrix} \right.$
步骤 2:代入向量表达式,化简得到等式
将向量表达式代入方程组,化简得到如下等式:
$\left \{ \begin{matrix} 0=-1\\ 4+5a=1\\ 1+6+2a=0\\ a=-\dfrac {3}{5}\end{matrix} \right.$
解得 $a=-\dfrac {3}{5}$。代入第二个方程中,得到:$4+5\times (-\dfrac {3}{5})=1\Longrightarrow 1=1=1$
这个等式恒成立。
步骤 3:求解线性表示式
根据线性表示的定义,我们要找到一组系数使得线性组合等于相应的向量。设系数为 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$,代入线性表示关系,得到方程组:
$\int {k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}+{k}_{3}{\alpha }_{3}=$ ${k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}+{k}_{3}{\alpha }_{3}=$
代入向量表达式,化简得到如下等式:
$\left \{ \begin{matrix} {k}_{1}+{k}_{2}+{k}_{3}=-1\\ {k}_{2}+2{k}_{3}=2\\ {k}_{1}+{k}_{2}+\dfrac {2}{5}{k}_{3}=1\\ {k}_{1}+2{k}_{2}-\dfrac { \right.$,解得:
${k}_{1}=\dfrac {3}{5}-\dfrac {7}{25}b$ ${k}_{2}=\dfrac {12}{5}-\dfrac {9}{25}b$ ${k}_{3}=-\dfrac {8}{5}+\dfrac {11}{25}b$
将 ${k}_{1}$, ${k}_{2}$, ${k}_{3}$ 代入线性表示关系,得到线性表示式为:
${\beta }_{1}=\left(\dfrac {3}{5}-\dfrac {7}{25}b\right){\alpha }_{1}+\left(\dfrac {12}{5}-\dfrac {9}{25}b\right){\alpha }_{2}+\left(-\dfrac {8}{5}+\dfrac {11}{25}b\right){\alpha }_{3}$
${\beta }_{2}=\left(\dfrac {3}{5}-\dfrac {7}{25}b\right){\alpha }_{1}+\left(\dfrac {12}{5}-\dfrac {9}{25}b\right){\alpha }_{2}+\left(-\dfrac {8}{5}+\dfrac {11}{25}b\right){\alpha }_{3}$