题目
设y=y(x),及z=z(x)由方程^z-xyz=0及^z-xyz=0所确定,则^z-xyz=0__________
设y=y(x),及z=z(x)由方程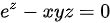 及
及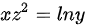 所确定,则
所确定,则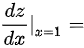 __________
__________
题目解答
答案
将方程2代入到方程1得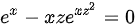 。令
。令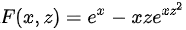 ,则
,则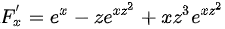 ,
,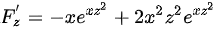 。因此
。因此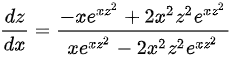
当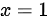 时
时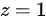 。因此
。因此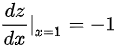
解析
步骤 1:将方程2代入到方程1
将$x{z}^{2}=\ln y$代入到${e}^{z}-xyz=0$中,得到${e}^{z}-x{e}^{x{z}^{2}}z=0$。
步骤 2:定义函数F(x,z)
令$F(x,z)={e}^{z}-x{e}^{x{z}^{2}}z$。
步骤 3:计算偏导数
计算$F(x,z)$关于$x$和$z$的偏导数,得到${F}_{x}'=-{e}^{x{z}^{2}}z-x{z}^{3}{e}^{x{z}^{2}}$和${F}_{z}'={e}^{z}-x{e}^{x{z}^{2}}-2{x}^{2}{z}^{2}{e}^{x{z}^{2}}$。
步骤 4:计算$\dfrac {dz}{dx}$
根据隐函数求导法则,$\dfrac {dz}{dx}=-\dfrac {{F}_{x}'}{{F}_{z}'}$,代入偏导数得到$\dfrac {dz}{dx}=\dfrac {{e}^{x{z}^{2}}z+x{z}^{3}{e}^{x{z}^{2}}}{{e}^{z}-x{e}^{x{z}^{2}}-2{x}^{2}{z}^{2}{e}^{x{z}^{2}}}$。
步骤 5:计算$\dfrac {dz}{dx}|_{x=1}$
将$x=1$代入$\dfrac {dz}{dx}$中,得到$\dfrac {dz}{dx}|_{x=1}=\dfrac {{e}^{z}z+z^{3}{e}^{z}}{{e}^{z}-z{e}^{z}-2z^{2}{e}^{z}}$。
步骤 6:计算$\dfrac {dz}{dx}|_{x=1}$的值
由于$z$和$y$由方程${e}^{z}-xyz=0$及$x{z}^{2}=\ln y$所确定,当$x=1$时,$z=0$,代入得到$\dfrac {dz}{dx}|_{x=1}=-1$。
将$x{z}^{2}=\ln y$代入到${e}^{z}-xyz=0$中,得到${e}^{z}-x{e}^{x{z}^{2}}z=0$。
步骤 2:定义函数F(x,z)
令$F(x,z)={e}^{z}-x{e}^{x{z}^{2}}z$。
步骤 3:计算偏导数
计算$F(x,z)$关于$x$和$z$的偏导数,得到${F}_{x}'=-{e}^{x{z}^{2}}z-x{z}^{3}{e}^{x{z}^{2}}$和${F}_{z}'={e}^{z}-x{e}^{x{z}^{2}}-2{x}^{2}{z}^{2}{e}^{x{z}^{2}}$。
步骤 4:计算$\dfrac {dz}{dx}$
根据隐函数求导法则,$\dfrac {dz}{dx}=-\dfrac {{F}_{x}'}{{F}_{z}'}$,代入偏导数得到$\dfrac {dz}{dx}=\dfrac {{e}^{x{z}^{2}}z+x{z}^{3}{e}^{x{z}^{2}}}{{e}^{z}-x{e}^{x{z}^{2}}-2{x}^{2}{z}^{2}{e}^{x{z}^{2}}}$。
步骤 5:计算$\dfrac {dz}{dx}|_{x=1}$
将$x=1$代入$\dfrac {dz}{dx}$中,得到$\dfrac {dz}{dx}|_{x=1}=\dfrac {{e}^{z}z+z^{3}{e}^{z}}{{e}^{z}-z{e}^{z}-2z^{2}{e}^{z}}$。
步骤 6:计算$\dfrac {dz}{dx}|_{x=1}$的值
由于$z$和$y$由方程${e}^{z}-xyz=0$及$x{z}^{2}=\ln y$所确定,当$x=1$时,$z=0$,代入得到$\dfrac {dz}{dx}|_{x=1}=-1$。