题目
求函数=sqrt [3](x)((x)^2-3x)的导数
求函数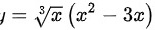 的导数
的导数
题目解答
答案
基本求导公式:
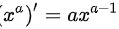
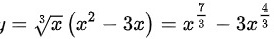
∴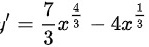
解析
步骤 1:将函数表达式转换为幂函数形式
将函数$y=\sqrt [3]{x}({x}^{2}-3x)$转换为幂函数形式,即$y={x}^{\dfrac {1}{3}}({x}^{2}-3x)$,进一步化简为$y={x}^{\dfrac {1}{3}}\cdot {x}^{2}-3{x}^{\dfrac {1}{3}}\cdot x$,即$y={x}^{\dfrac {7}{3}}-3{x}^{\dfrac {4}{3}}$。
步骤 2:应用幂函数的求导公式
根据幂函数的求导公式$({x}^{a})'=a{x}^{a-1}$,对$y={x}^{\dfrac {7}{3}}-3{x}^{\dfrac {4}{3}}$求导,得到$y'=\dfrac {7}{3}{x}^{\dfrac {7}{3}-1}-3\cdot \dfrac {4}{3}{x}^{\dfrac {4}{3}-1}$。
步骤 3:化简求导结果
化简求导结果,得到$y'=\dfrac {7}{3}{x}^{\dfrac {4}{3}}-4{x}^{\dfrac {1}{3}}$。
将函数$y=\sqrt [3]{x}({x}^{2}-3x)$转换为幂函数形式,即$y={x}^{\dfrac {1}{3}}({x}^{2}-3x)$,进一步化简为$y={x}^{\dfrac {1}{3}}\cdot {x}^{2}-3{x}^{\dfrac {1}{3}}\cdot x$,即$y={x}^{\dfrac {7}{3}}-3{x}^{\dfrac {4}{3}}$。
步骤 2:应用幂函数的求导公式
根据幂函数的求导公式$({x}^{a})'=a{x}^{a-1}$,对$y={x}^{\dfrac {7}{3}}-3{x}^{\dfrac {4}{3}}$求导,得到$y'=\dfrac {7}{3}{x}^{\dfrac {7}{3}-1}-3\cdot \dfrac {4}{3}{x}^{\dfrac {4}{3}-1}$。
步骤 3:化简求导结果
化简求导结果,得到$y'=\dfrac {7}{3}{x}^{\dfrac {4}{3}}-4{x}^{\dfrac {1}{3}}$。