题目
证明:ln dfrac (1+x)(1-x)+cos xgeqslant 1+dfrac ({x)^2}(2) -1lt xlt 1.
证明: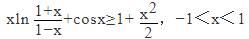 .
.
题目解答
答案

解析
步骤 1:定义函数
定义函数 $f(x)=x\ln \dfrac {1+x}{1-x}+\cos x-1-\dfrac {{x}^{2}}{2}$,其中 $-1\lt x\lt 1$。
步骤 2:验证函数的奇偶性
由于 $f(-x)=f(x)$,所以函数 $f(x)$ 是偶函数,因此只需讨论 $x\geqslant 0$ 的情况。
步骤 3:计算一阶导数
计算 $f(x)$ 的一阶导数 $f'(x)$,得到 $f'(x)=\ln \dfrac {1+x}{1-x}+\dfrac {2x}{1-{x}^{2}}-\sin x-x$。
步骤 4:计算二阶导数
计算 $f'(x)$ 的一阶导数 $f''(x)$,得到 $f''(x)=\dfrac {4}{{(1-{x}^{2})}^{2}}-\cos x-1$。
步骤 5:分析二阶导数的符号
当 $x\in (0,1)$ 时,$f''(x)\geqslant 0$,因此 $f'(x)$ 在 $x\in (0,1)$ 上单调递增。
步骤 6:分析一阶导数的符号
由于 $f'(0)=2\gt 0$,因此 $f'(x)\geqslant 0$,所以 $f(x)$ 在 $x\in [0,1)$ 上单调递增。
步骤 7:分析函数的符号
由于 $f(0)=0$,因此 $f(x)\geqslant 0$,即 $x\ln \dfrac {1+x}{1-x}+\cos x\geqslant 1+\dfrac {{x}^{2}}{2}$。
定义函数 $f(x)=x\ln \dfrac {1+x}{1-x}+\cos x-1-\dfrac {{x}^{2}}{2}$,其中 $-1\lt x\lt 1$。
步骤 2:验证函数的奇偶性
由于 $f(-x)=f(x)$,所以函数 $f(x)$ 是偶函数,因此只需讨论 $x\geqslant 0$ 的情况。
步骤 3:计算一阶导数
计算 $f(x)$ 的一阶导数 $f'(x)$,得到 $f'(x)=\ln \dfrac {1+x}{1-x}+\dfrac {2x}{1-{x}^{2}}-\sin x-x$。
步骤 4:计算二阶导数
计算 $f'(x)$ 的一阶导数 $f''(x)$,得到 $f''(x)=\dfrac {4}{{(1-{x}^{2})}^{2}}-\cos x-1$。
步骤 5:分析二阶导数的符号
当 $x\in (0,1)$ 时,$f''(x)\geqslant 0$,因此 $f'(x)$ 在 $x\in (0,1)$ 上单调递增。
步骤 6:分析一阶导数的符号
由于 $f'(0)=2\gt 0$,因此 $f'(x)\geqslant 0$,所以 $f(x)$ 在 $x\in [0,1)$ 上单调递增。
步骤 7:分析函数的符号
由于 $f(0)=0$,因此 $f(x)\geqslant 0$,即 $x\ln \dfrac {1+x}{1-x}+\cos x\geqslant 1+\dfrac {{x}^{2}}{2}$。