题目
lim _(narrow infty )(1+dfrac (1)(2)+dfrac (1)(4)+... +dfrac (1)({2)^n})
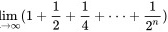
题目解答
答案
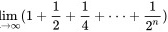
=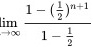
=2
解析
步骤 1:识别数列类型
数列 $1+\dfrac {1}{2}+\dfrac {1}{4}+\cdots +\dfrac {1}{{2}^{n}}$ 是一个等比数列,其中首项 $a_1=1$,公比 $q=\dfrac{1}{2}$。
步骤 2:应用等比数列求和公式
等比数列的前 $n$ 项和公式为 $S_n=\dfrac{a_1(1-q^n)}{1-q}$。将 $a_1=1$ 和 $q=\dfrac{1}{2}$ 代入公式,得到 $S_n=\dfrac{1(1-(\dfrac{1}{2})^n)}{1-\dfrac{1}{2}}$。
步骤 3:计算极限
当 $n$ 趋于无穷大时,$(\dfrac{1}{2})^n$ 趋于 $0$,因此 $\lim _{n\rightarrow \infty }S_n=\lim _{n\rightarrow \infty }\dfrac{1(1-(\dfrac{1}{2})^n)}{1-\dfrac{1}{2}}=\dfrac{1(1-0)}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2$。
数列 $1+\dfrac {1}{2}+\dfrac {1}{4}+\cdots +\dfrac {1}{{2}^{n}}$ 是一个等比数列,其中首项 $a_1=1$,公比 $q=\dfrac{1}{2}$。
步骤 2:应用等比数列求和公式
等比数列的前 $n$ 项和公式为 $S_n=\dfrac{a_1(1-q^n)}{1-q}$。将 $a_1=1$ 和 $q=\dfrac{1}{2}$ 代入公式,得到 $S_n=\dfrac{1(1-(\dfrac{1}{2})^n)}{1-\dfrac{1}{2}}$。
步骤 3:计算极限
当 $n$ 趋于无穷大时,$(\dfrac{1}{2})^n$ 趋于 $0$,因此 $\lim _{n\rightarrow \infty }S_n=\lim _{n\rightarrow \infty }\dfrac{1(1-(\dfrac{1}{2})^n)}{1-\dfrac{1}{2}}=\dfrac{1(1-0)}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2$。