题目
lim _(narrow infty )(2)^nsin dfrac (x)({2)^n}-|||-__(x为不等于零的常数)
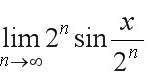($$x$$为不等于零的常数)
题目解答
答案
因为$$\frac{x}{2^n}$$和$$\sin\frac{x}{2^n}$$是等价无穷小，
所以当$$n\rightarrow\infty $$时
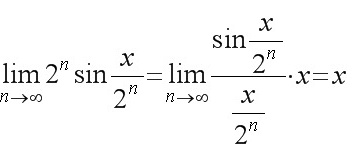
解析
步骤 1：等价无穷小替换
当$$n\rightarrow\infty$$时，$$\frac{x}{2^n}$$趋于0，因此$$\sin\frac{x}{2^n}$$和$$\frac{x}{2^n}$$是等价无穷小。这意味着$$\sin\frac{x}{2^n}$$可以被$$\frac{x}{2^n}$$替换，因为它们在$$n\rightarrow\infty$$时的比值趋于1。
步骤 2：替换并简化
将$$\sin\frac{x}{2^n}$$替换为$$\frac{x}{2^n}$$，得到$$2^n\cdot\frac{x}{2^n}$$。这可以简化为$$x$$。
步骤 3：计算极限
由于$$2^n\cdot\frac{x}{2^n}$$简化为$$x$$，所以$$\lim _{n\rightarrow \infty }{2}^{n}\sin \dfrac {x}{{2}^{n}}$$等于$$x$$。
当$$n\rightarrow\infty$$时，$$\frac{x}{2^n}$$趋于0，因此$$\sin\frac{x}{2^n}$$和$$\frac{x}{2^n}$$是等价无穷小。这意味着$$\sin\frac{x}{2^n}$$可以被$$\frac{x}{2^n}$$替换，因为它们在$$n\rightarrow\infty$$时的比值趋于1。
步骤 2：替换并简化
将$$\sin\frac{x}{2^n}$$替换为$$\frac{x}{2^n}$$，得到$$2^n\cdot\frac{x}{2^n}$$。这可以简化为$$x$$。
步骤 3：计算极限
由于$$2^n\cdot\frac{x}{2^n}$$简化为$$x$$，所以$$\lim _{n\rightarrow \infty }{2}^{n}\sin \dfrac {x}{{2}^{n}}$$等于$$x$$。