题目
3.设函数 f(x)= { ,xgt 0 ln (1+x),-1lt xleqslant 0 . 求f(x)函数的间断点,并分析间断点的类型.
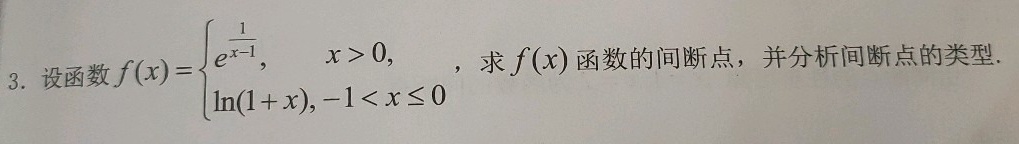
题目解答
答案

解析
步骤 1:确定可能的间断点
函数f(x)在x=0和x=1处可能有间断点,因为函数在这些点处的定义发生了变化。
步骤 2:分析x=0处的间断点
- 左极限:$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \ln(1+x) = \ln(1) = 0$
- 右极限:$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} e^{\frac{1}{x-1}} = e^{-\infty} = 0$
- 函数值:$f(0) = \ln(1+0) = 0$
由于左极限、右极限和函数值都相等,所以x=0处不是间断点。
步骤 3:分析x=1处的间断点
- 左极限:$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} e^{\frac{1}{x-1}} = e^{+\infty} = +\infty$
- 右极限:$\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} e^{\frac{1}{x-1}} = e^{+\infty} = +\infty$
- 函数值:函数在x=1处没有定义。
由于左极限和右极限都为无穷大,所以x=1处为无穷间断点(第二类)。
函数f(x)在x=0和x=1处可能有间断点,因为函数在这些点处的定义发生了变化。
步骤 2:分析x=0处的间断点
- 左极限:$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \ln(1+x) = \ln(1) = 0$
- 右极限:$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} e^{\frac{1}{x-1}} = e^{-\infty} = 0$
- 函数值:$f(0) = \ln(1+0) = 0$
由于左极限、右极限和函数值都相等,所以x=0处不是间断点。
步骤 3:分析x=1处的间断点
- 左极限:$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} e^{\frac{1}{x-1}} = e^{+\infty} = +\infty$
- 右极限:$\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} e^{\frac{1}{x-1}} = e^{+\infty} = +\infty$
- 函数值:函数在x=1处没有定义。
由于左极限和右极限都为无穷大,所以x=1处为无穷间断点(第二类)。