题目

下面哪个方程在 [ 0 , 1 ] 内有实根A.+tan x+dfrac (1)(4)=0A.+tan x+dfrac (1)(4)=0A.+tan x+dfrac (1)(4)=0A.+tan x+dfrac (1)(4)=0

下面哪个方程在 [ 0 , 1 ] 内有实根

$A.x+\tan x+\frac{1}{4}=0$

$B.\frac{1}{2}x-\tan x-1=0$

$C.3x^2+x+1=0$

$D.x+\tan x-\frac{1}{4}=0$

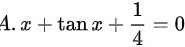
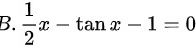
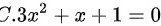
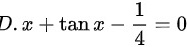
题目解答

答案

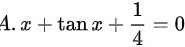$A.x+\tan x+\frac{1}{4}=0$ ，可得：函数在区间内单调递增，故最小值为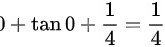： $0+\tan0+\frac{1}{4}=\frac{1}{4}$ ，故无实根，故选项A错误。

$B.\frac{1}{2}x-\tan x-1=0$ ，可得：

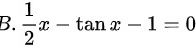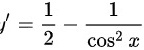$y'=\frac{1}{2}-\frac{1}{\cos^2x}$ ，可得：函数在区间内单调递减，故最小值为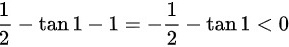： $\frac{1}{2}-\tan1-1=-\frac{1}{2}-\tan1<0$ ，最大值为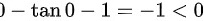： $0-\tan0-1=-1<0$ ，故无实根，故选项B错误。

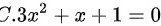$C.3x^2+x+1=0$ ，可得在区间[ 0 , 1 ] 内函数恒大于0，故函数无实根，故选项C错误。

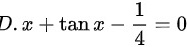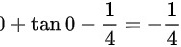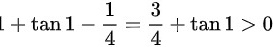$D.x+\tan x-\frac{1}{4}=0$ ，可得：函数在区间内单调递增，故最小值为： $0+\tan0-\frac{1}{4}=-\frac{1}{4}$ ，最大值为 $1+\tan1-\frac{1}{4}=\frac{3}{4}+\tan1>0$ ，故有实根，故选项D正确。

故本题的正确答案为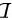 $D$

解析

步骤 1：分析方程 A
方程 A 为 $x+\tan x+\dfrac {1}{4}=0$。在区间 [0, 1] 内，$x$ 和 $\tan x$ 都是单调递增的，因此整个函数也是单调递增的。在 $x=0$ 时，函数值为 $\dfrac {1}{4}$，在 $x=1$ 时，函数值为 $1+\tan 1+\dfrac {1}{4}$，显然大于 0。因此，方程 A 在 [0, 1] 内没有实根。

步骤 2：分析方程 B
方程 B 为 $\dfrac {1}{2}x-\tan x-1=0$。在区间 [0, 1] 内，$\dfrac {1}{2}x$ 是单调递增的，而 $\tan x$ 也是单调递增的，因此整个函数是单调递减的。在 $x=0$ 时，函数值为 $-1$，在 $x=1$ 时，函数值为 $\dfrac {1}{2}-\tan 1-1$，显然小于 0。因此，方程 B 在 [0, 1] 内没有实根。

步骤 3：分析方程 C
方程 C 为 $3{x}^{2}+x+1=0$。这是一个二次方程，其判别式 $\Delta = 1^2 - 4 \cdot 3 \cdot 1 = 1 - 12 = -11$，小于 0，因此方程 C 没有实根。

步骤 4：分析方程 D
方程 D 为 $x+\tan x-\dfrac {1}{4}=0$。在区间 [0, 1] 内，$x$ 和 $\tan x$ 都是单调递增的，因此整个函数也是单调递增的。在 $x=0$ 时，函数值为 $-\dfrac {1}{4}$，在 $x=1$ 时，函数值为 $1+\tan 1-\dfrac {1}{4}$，显然大于 0。因此，方程 D 在 [0, 1] 内有实根。