题目
(13)设 lim _(xarrow 1)dfrac ({x)^3+ax-2}({x)^2-1}=2 求a的值。
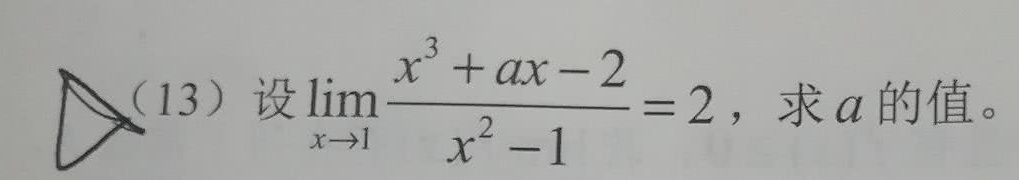
题目解答
答案

解析
步骤 1:确定极限存在的条件
由于 $\lim _{x\rightarrow 1}\dfrac {{x}^{3}+ax-2}{{x}^{2}-1}=2$ 存在,且分母在 $x=1$ 时为零,因此分子在 $x=1$ 时也必须为零,以保证极限存在。这意味着 $x=1$ 是分子多项式 ${x}^{3}+ax-2$ 的一个根。
步骤 2:求解a的值
将 $x=1$ 代入分子多项式 ${x}^{3}+ax-2$,得到 $1^3 + a \cdot 1 - 2 = 0$,即 $1 + a - 2 = 0$。解这个方程得到 $a = 1$。
步骤 3:验证极限值
将 $a=1$ 代入原极限表达式,得到 $\lim _{x\rightarrow 1}\dfrac {{x}^{3}+x-2}{{x}^{2}-1}$。分子可以因式分解为 $(x-1)(x^2+x+2)$,分母可以因式分解为 $(x-1)(x+1)$。因此,原极限表达式可以简化为 $\lim _{x\rightarrow 1}\dfrac {(x-1)(x^2+x+2)}{(x-1)(x+1)}$。在 $x\neq 1$ 的情况下,可以约去 $(x-1)$,得到 $\lim _{x\rightarrow 1}\dfrac {x^2+x+2}{x+1}$。将 $x=1$ 代入,得到 $\dfrac {1^2+1+2}{1+1} = \dfrac {4}{2} = 2$,与题目给定的极限值一致。
由于 $\lim _{x\rightarrow 1}\dfrac {{x}^{3}+ax-2}{{x}^{2}-1}=2$ 存在,且分母在 $x=1$ 时为零,因此分子在 $x=1$ 时也必须为零,以保证极限存在。这意味着 $x=1$ 是分子多项式 ${x}^{3}+ax-2$ 的一个根。
步骤 2:求解a的值
将 $x=1$ 代入分子多项式 ${x}^{3}+ax-2$,得到 $1^3 + a \cdot 1 - 2 = 0$,即 $1 + a - 2 = 0$。解这个方程得到 $a = 1$。
步骤 3:验证极限值
将 $a=1$ 代入原极限表达式,得到 $\lim _{x\rightarrow 1}\dfrac {{x}^{3}+x-2}{{x}^{2}-1}$。分子可以因式分解为 $(x-1)(x^2+x+2)$,分母可以因式分解为 $(x-1)(x+1)$。因此,原极限表达式可以简化为 $\lim _{x\rightarrow 1}\dfrac {(x-1)(x^2+x+2)}{(x-1)(x+1)}$。在 $x\neq 1$ 的情况下,可以约去 $(x-1)$,得到 $\lim _{x\rightarrow 1}\dfrac {x^2+x+2}{x+1}$。将 $x=1$ 代入,得到 $\dfrac {1^2+1+2}{1+1} = \dfrac {4}{2} = 2$,与题目给定的极限值一致。