题目
1.求下列极限:(2)lim _(xarrow dfrac {pi )(2)}dfrac (ln sin x)({(pi -2x))^2}
1.求下列极限:
(2)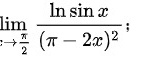
题目解答
答案
在本题中,根据常见的等价无穷小: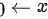 时,
时,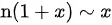 ,且
,且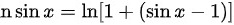 ,
,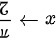 时,
时,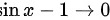 ,可得到
,可得到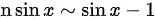 ,因此原极限可化为:
,因此原极限可化为: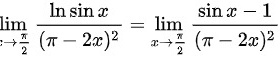 .由于
.由于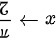 时,
时,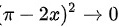 ,因此,根据洛必达法则:
,因此,根据洛必达法则:
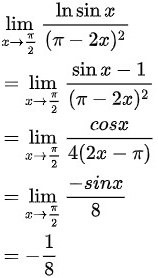
原极限的值为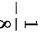 .
.
解析
步骤 1:等价无穷小替换
当$x\rightarrow \dfrac {\pi }{2}$时,$\sin x\rightarrow 1$,因此$\ln \sin x$可以使用等价无穷小替换,即$\ln \sin x\sim \sin x-1$。这是因为当$x\rightarrow 0$时,$\ln(1+x)\sim x$,而$\sin x-1$在$x\rightarrow \dfrac {\pi }{2}$时趋于0,所以$\ln \sin x\sim \sin x-1$。
步骤 2:代入等价无穷小
将$\ln \sin x$替换为$\sin x-1$,原极限变为$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {\sin x-1}{{(\pi -2x)}^{2}}$。
步骤 3:应用洛必达法则
由于分子和分母在$x\rightarrow \dfrac {\pi }{2}$时都趋于0,可以应用洛必达法则。对分子和分母分别求导,得到$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {\cos x}{-4(\pi -2x)}$。再次应用洛必达法则,得到$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {-\sin x}{8}$。将$x=\dfrac {\pi }{2}$代入,得到$\dfrac {-\sin \dfrac {\pi }{2}}{8}=-\dfrac {1}{8}$。
当$x\rightarrow \dfrac {\pi }{2}$时,$\sin x\rightarrow 1$,因此$\ln \sin x$可以使用等价无穷小替换,即$\ln \sin x\sim \sin x-1$。这是因为当$x\rightarrow 0$时,$\ln(1+x)\sim x$,而$\sin x-1$在$x\rightarrow \dfrac {\pi }{2}$时趋于0,所以$\ln \sin x\sim \sin x-1$。
步骤 2:代入等价无穷小
将$\ln \sin x$替换为$\sin x-1$,原极限变为$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {\sin x-1}{{(\pi -2x)}^{2}}$。
步骤 3:应用洛必达法则
由于分子和分母在$x\rightarrow \dfrac {\pi }{2}$时都趋于0,可以应用洛必达法则。对分子和分母分别求导,得到$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {\cos x}{-4(\pi -2x)}$。再次应用洛必达法则,得到$\lim _{x\rightarrow \dfrac {\pi }{2}}\dfrac {-\sin x}{8}$。将$x=\dfrac {\pi }{2}$代入,得到$\dfrac {-\sin \dfrac {\pi }{2}}{8}=-\dfrac {1}{8}$。