题目

(int )_(0)^dfrac (pi {4)}dfrac (x)(1+cos 2x)dx=( ) .(int )_(0)^dfrac (pi {4)}dfrac (x)(1+cos 2x)dx=(int )_(0)^dfrac (pi {4)}dfrac (x)(1+cos 2x)dx=(int )_(0)^dfrac (pi {4)}dfrac (x)(1+cos 2x)dx=(int )_(0)^dfrac (pi {4)}dfrac (x)(1+cos 2x)dx=

$\int_{0}^{\frac{\pi}{4}} \frac{x}{1+\cos 2 x} {d} x=$ ( ) .

$A. \frac{\pi}{8}+\frac{\ln 2}{4}$

$B.\frac{\pi}{8}-\frac{\ln 2}{4}$

$C. \frac{\pi}{4}-\frac{\ln 2}{8}$

$D. \frac{\pi}{4}+\frac{\ln 2}{8}$

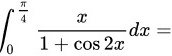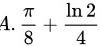
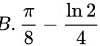
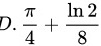
题目解答

答案

由题意得，

利用分部积分法有，

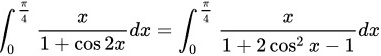
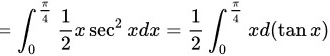
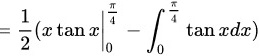
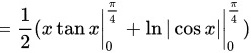
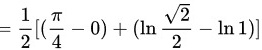
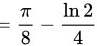$\int_0^{\frac{\pi}{4}}\frac{x}{1+\cos2x}dx=\int_0^{\frac{\pi}{4}}\frac{x}{1+2\cos^2x-1}dx$ $=\int_0^{\frac{\pi}{4}}\frac{1}{2}x\sec^2xdx=\frac{1}{2}\int_0^{\frac{\pi}{4}}xd(\tan x)$ $=\frac{1}{2}(x\tan x\bigg|_0^{\frac{\pi}{4}}-\int_0^{\frac{\pi}{4}} \tan xdx)$ $=\frac{1}{2}(x\tan x\bigg|_0^{\frac{\pi}{4}}+\ln|\cos x|\bigg|_0^{\frac{\pi}{4}})$ $=\frac{1}{2}[(\frac{\pi}{4}-0)+(\ln\frac{\sqrt{2}}{2}-\ln1)]$

$=\frac{\pi}{8}-\frac{\ln2}{4}$ 。

故答案选 $B$ .

解析

步骤 1：化简被积函数
利用三角恒等式 $1 + \cos 2x = 2\cos^2 x$，将被积函数化简为 $\dfrac{x}{2\cos^2 x}$。
步骤 2：应用分部积分法
将 $\dfrac{x}{2\cos^2 x}$ 写成 $\dfrac{1}{2}x\sec^2 x$，并应用分部积分法，设 $u = x$，$dv = \sec^2 x dx$，则 $du = dx$，$v = \tan x$。
步骤 3：计算积分
根据分部积分法，原积分变为 $\dfrac{1}{2}x\tan x{\int }_{0}^{\dfrac {\pi }{4}} - \dfrac{1}{2}{\int }_{0}^{\dfrac {\pi }{4}}\tan x dx$。计算 $\tan x$ 的积分，得到 $\ln|\cos x|$。
步骤 4：代入上下限
将上下限代入，得到 $\dfrac{1}{2}(\dfrac{\pi}{4}\tan\dfrac{\pi}{4} - 0) + \dfrac{1}{2}(\ln|\cos\dfrac{\pi}{4}| - \ln|\cos 0|)$。
步骤 5：化简结果
化简得到 $\dfrac{\pi}{8} - \dfrac{\ln 2}{4}$。