题目
求下列函数的导数: (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4; (1) =((2x+5))^4.
求下列函数的导数:
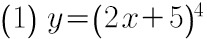 ;
;
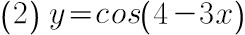 ;
;
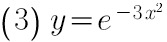 ;
;
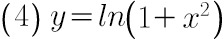 ;
;
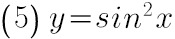 ;
;
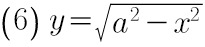 ;
;
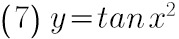 ;
;
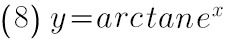 ;
;
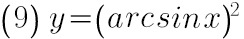 ;
;
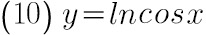 .
.
题目解答
答案
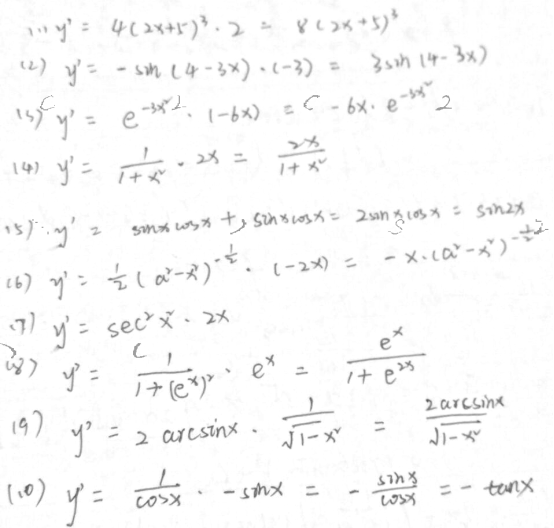
解析
步骤 1:求导数
(1) $y={(2x+5)}^{4}$;
$y'=4{(2x+5)}^{3}\cdot 2=8{(2x+5)}^{3}$
(2) $y=\cos (4-3x)$;
$y'=-\sin (4-3x)\cdot (-3)=3\sin (4-3x)$
(3) $y={e}^{-3{x}^{2}}$;
$y'={e}^{-3{x}^{2}}\cdot (-6x)=-6x\cdot {e}^{-3{x}^{2}}$
(4) $y=\ln (1+{x}^{2})$;
$y'=\dfrac {1}{1+{x}^{2}}\cdot 2x=\dfrac {2x}{1+{x}^{2}}$
(5) $y={\sin }^{2}x$;
$y'=2\sin x\cos x=\sin 2x$
(6) $y=\sqrt {{a}^{2}-{x}^{2}}$;
$y'=\dfrac {1}{2}{({a}^{2}-{x}^{2})}^{-\dfrac {1}{2}}\cdot (-2x)=-\dfrac {x}{\sqrt {{a}^{2}-{x}^{2}}}$
(7) $y=\tan {x}^{2}$;
$y'={\sec }^{2}{x}^{2}\cdot 2x=2x{\sec }^{2}{x}^{2}$
(8) $y=\arctan {e}^{x}$;
$y'=\dfrac {1}{1+{e}^{2x}}\cdot {e}^{x}=\dfrac {{e}^{x}}{1+{e}^{2x}}$
(9) $y={(\arcsin x)}^{2}$;
$y'=2\arcsin x\cdot \dfrac {1}{\sqrt {1-{x}^{2}}}=\dfrac {2\arcsin x}{\sqrt {1-{x}^{2}}}$
(10) $y=\ln \cos x$;
$y'=\dfrac {1}{\cos x}\cdot (-\sin x)=-\dfrac {\sin x}{\cos x}=-\tan x$
(1) $y={(2x+5)}^{4}$;
$y'=4{(2x+5)}^{3}\cdot 2=8{(2x+5)}^{3}$
(2) $y=\cos (4-3x)$;
$y'=-\sin (4-3x)\cdot (-3)=3\sin (4-3x)$
(3) $y={e}^{-3{x}^{2}}$;
$y'={e}^{-3{x}^{2}}\cdot (-6x)=-6x\cdot {e}^{-3{x}^{2}}$
(4) $y=\ln (1+{x}^{2})$;
$y'=\dfrac {1}{1+{x}^{2}}\cdot 2x=\dfrac {2x}{1+{x}^{2}}$
(5) $y={\sin }^{2}x$;
$y'=2\sin x\cos x=\sin 2x$
(6) $y=\sqrt {{a}^{2}-{x}^{2}}$;
$y'=\dfrac {1}{2}{({a}^{2}-{x}^{2})}^{-\dfrac {1}{2}}\cdot (-2x)=-\dfrac {x}{\sqrt {{a}^{2}-{x}^{2}}}$
(7) $y=\tan {x}^{2}$;
$y'={\sec }^{2}{x}^{2}\cdot 2x=2x{\sec }^{2}{x}^{2}$
(8) $y=\arctan {e}^{x}$;
$y'=\dfrac {1}{1+{e}^{2x}}\cdot {e}^{x}=\dfrac {{e}^{x}}{1+{e}^{2x}}$
(9) $y={(\arcsin x)}^{2}$;
$y'=2\arcsin x\cdot \dfrac {1}{\sqrt {1-{x}^{2}}}=\dfrac {2\arcsin x}{\sqrt {1-{x}^{2}}}$
(10) $y=\ln \cos x$;
$y'=\dfrac {1}{\cos x}\cdot (-\sin x)=-\dfrac {\sin x}{\cos x}=-\tan x$