题目
[题目]-|||-求微分方程 '=((y'))^3+y' 的通解.
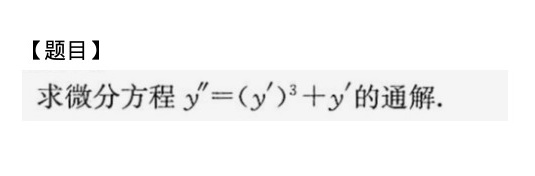
题目解答
答案

解析
步骤 1:引入变量
令 $y'=p$,则 $y''=\dfrac{dp}{dx}=\dfrac{dp}{dy}\dfrac{dy}{dx}=p\dfrac{dp}{dy}$。代入原方程得到 $p\dfrac{dp}{dy}={p}^{3}+p$。
步骤 2:分离变量
将方程 $p\dfrac{dp}{dy}={p}^{3}+p$ 分离变量,得到 $\dfrac{dp}{1+{p}^{2}}=dy$。
步骤 3:积分求解
对分离变量后的方程两边积分,得到 $\int \dfrac{dp}{1+{p}^{2}}=\int dy$,即 $\arctan p=y+C_1$。由此得到 $p=\tan(y+C_1)$。
步骤 4:回代求解
由 $p=y'$,得到 $\dfrac{dy}{dx}=\tan(y+C_1)$。分离变量得到 $\dfrac{dy}{\tan(y+C_1)}=dx$,即 $\ln|\sin(y+C_1)|=x+C_2$。由此得到 $y=C_1+\arcsin(e^{C_2}e^x)$。
令 $y'=p$,则 $y''=\dfrac{dp}{dx}=\dfrac{dp}{dy}\dfrac{dy}{dx}=p\dfrac{dp}{dy}$。代入原方程得到 $p\dfrac{dp}{dy}={p}^{3}+p$。
步骤 2:分离变量
将方程 $p\dfrac{dp}{dy}={p}^{3}+p$ 分离变量,得到 $\dfrac{dp}{1+{p}^{2}}=dy$。
步骤 3:积分求解
对分离变量后的方程两边积分,得到 $\int \dfrac{dp}{1+{p}^{2}}=\int dy$,即 $\arctan p=y+C_1$。由此得到 $p=\tan(y+C_1)$。
步骤 4:回代求解
由 $p=y'$,得到 $\dfrac{dy}{dx}=\tan(y+C_1)$。分离变量得到 $\dfrac{dy}{\tan(y+C_1)}=dx$,即 $\ln|\sin(y+C_1)|=x+C_2$。由此得到 $y=C_1+\arcsin(e^{C_2}e^x)$。