题目
求下列极限lim _(xarrow {0)^+}((1+dfrac {1)(x))}^x
求下列极限
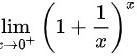
题目解答
答案
极限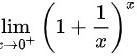
该极限满足了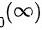
的形式，
则极限转化为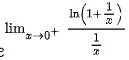
令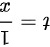
,得到极限为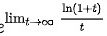
利用洛必达法则，得到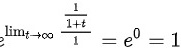
所以本题答案为1
解析
步骤 1：确定极限形式
观察极限$\lim _{x\rightarrow {0}^{+}}{(1+\dfrac {1}{x})}^{x}$，发现它满足${(x)}^{0}$的形式，即当$x$趋近于$0$时，底数$(1+\dfrac {1}{x})$趋近于无穷大，而指数$x$趋近于$0$。这种形式的极限通常需要转换成指数函数的形式来求解。
步骤 2：转换成指数函数形式
为了方便求解，我们首先将原极限转换成指数函数的形式。利用对数的性质，可以将原极限写成$\lim _{x\rightarrow {0}^{+}}e^{x\ln(1+\dfrac {1}{x})}$。这样，问题就转化为了求解$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})$。
步骤 3：利用洛必达法则求解
观察$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})$，发现它满足$\dfrac{0}{0}$的不定式形式。因此，可以使用洛必达法则来求解。首先，令$t=\dfrac {1}{x}$，则$x=\dfrac {1}{t}$，当$x\rightarrow {0}^{+}$时，$t\rightarrow {+\infty}$。因此，原极限可以写成$\lim _{t\rightarrow {+\infty}}\dfrac{\ln(1+t)}{t}$。接下来，应用洛必达法则，求导数得到$\lim _{t\rightarrow {+\infty}}\dfrac{\dfrac{1}{1+t}}{1}=\lim _{t\rightarrow {+\infty}}\dfrac{1}{1+t}=0$。因此，$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})=0$。
步骤 4：求解原极限
根据步骤3的结果，$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})=0$，因此原极限$\lim _{x\rightarrow {0}^{+}}e^{x\ln(1+\dfrac {1}{x})}=e^{0}=1$。
观察极限$\lim _{x\rightarrow {0}^{+}}{(1+\dfrac {1}{x})}^{x}$，发现它满足${(x)}^{0}$的形式，即当$x$趋近于$0$时，底数$(1+\dfrac {1}{x})$趋近于无穷大，而指数$x$趋近于$0$。这种形式的极限通常需要转换成指数函数的形式来求解。
步骤 2：转换成指数函数形式
为了方便求解，我们首先将原极限转换成指数函数的形式。利用对数的性质，可以将原极限写成$\lim _{x\rightarrow {0}^{+}}e^{x\ln(1+\dfrac {1}{x})}$。这样，问题就转化为了求解$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})$。
步骤 3：利用洛必达法则求解
观察$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})$，发现它满足$\dfrac{0}{0}$的不定式形式。因此，可以使用洛必达法则来求解。首先，令$t=\dfrac {1}{x}$，则$x=\dfrac {1}{t}$，当$x\rightarrow {0}^{+}$时，$t\rightarrow {+\infty}$。因此，原极限可以写成$\lim _{t\rightarrow {+\infty}}\dfrac{\ln(1+t)}{t}$。接下来，应用洛必达法则，求导数得到$\lim _{t\rightarrow {+\infty}}\dfrac{\dfrac{1}{1+t}}{1}=\lim _{t\rightarrow {+\infty}}\dfrac{1}{1+t}=0$。因此，$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})=0$。
步骤 4：求解原极限
根据步骤3的结果，$\lim _{x\rightarrow {0}^{+}}x\ln(1+\dfrac {1}{x})=0$，因此原极限$\lim _{x\rightarrow {0}^{+}}e^{x\ln(1+\dfrac {1}{x})}=e^{0}=1$。