题目
设α,β,y线性无关.证明 +beta , +y , +a 也线性无关.
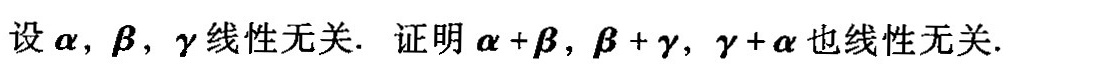
题目解答
答案

解析
步骤 1:假设线性相关
假设 $\alpha +\beta $ ,$\beta +\gamma $ , $y+a$ 线性相关,那么存在不全为0的数 $k_1$ , $k_2$ , $k_3$ 使得
$$
k_1(\alpha +\beta )+k_2(\beta +\gamma )+k_3(y+\alpha )=0
$$
步骤 2:整理方程
将上述方程整理,得到
$$
(k_1+k_3)\alpha + (k_1+k_2)\beta + (k_2+k_3)\gamma = 0
$$
步骤 3:利用线性无关的性质
由于 $\alpha$ , $\beta$ , $\gamma$ 线性无关,所以系数必须满足
$$
\left \{ \begin{matrix} k_1+k_3=0\\ k_1+k_2=0\\ k_2+k_3=0\end{matrix} \right.
$$
步骤 4:解方程组
解上述方程组,得到
$$
k_1=k_2=k_3=0
$$
步骤 5:得出矛盾
这与假设 $k_1$ , $k_2$ , $k_3$ 不全为0相矛盾,因此假设不成立。
假设 $\alpha +\beta $ ,$\beta +\gamma $ , $y+a$ 线性相关,那么存在不全为0的数 $k_1$ , $k_2$ , $k_3$ 使得
$$
k_1(\alpha +\beta )+k_2(\beta +\gamma )+k_3(y+\alpha )=0
$$
步骤 2:整理方程
将上述方程整理,得到
$$
(k_1+k_3)\alpha + (k_1+k_2)\beta + (k_2+k_3)\gamma = 0
$$
步骤 3:利用线性无关的性质
由于 $\alpha$ , $\beta$ , $\gamma$ 线性无关,所以系数必须满足
$$
\left \{ \begin{matrix} k_1+k_3=0\\ k_1+k_2=0\\ k_2+k_3=0\end{matrix} \right.
$$
步骤 4:解方程组
解上述方程组,得到
$$
k_1=k_2=k_3=0
$$
步骤 5:得出矛盾
这与假设 $k_1$ , $k_2$ , $k_3$ 不全为0相矛盾,因此假设不成立。