题目
已知函数(x)=tan x,则(x)=tan x ____ ．
已知函数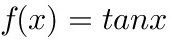
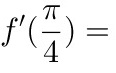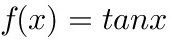,则
____ ．
,则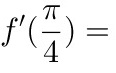 ____ ．题目解答
答案
2
解: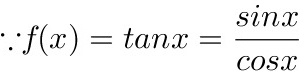
,
,
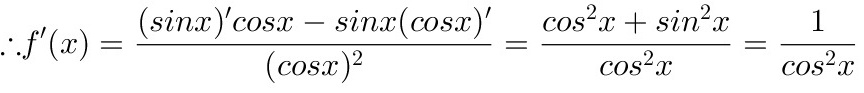则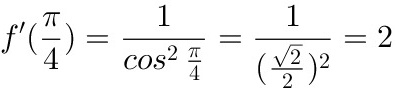
,
故答案为:2
解:
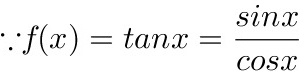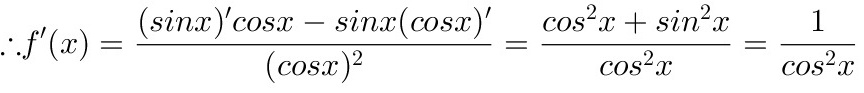,,则
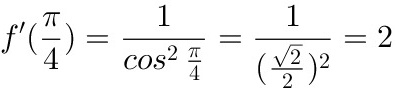,故答案为:2
解析
步骤 1：求导
首先，我们需要求出函数$f(x)=\tan x$的导数$f'(x)$。根据导数的定义和三角函数的导数公式，我们知道$\tan x$的导数是$\sec^2 x$，即$f'(x)=\sec^2 x$。
步骤 2：代入求值
接下来，我们需要计算$f'(\dfrac {\pi }{4})$的值。根据步骤1中得到的导数公式，我们只需将$x=\dfrac {\pi }{4}$代入$f'(x)=\sec^2 x$中。
步骤 3：计算结果
由于$\sec x = \dfrac{1}{\cos x}$，所以$\sec^2 x = \dfrac{1}{\cos^2 x}$。当$x=\dfrac {\pi }{4}$时，$\cos \dfrac {\pi }{4} = \dfrac{\sqrt{2}}{2}$，因此$\sec^2 \dfrac {\pi }{4} = \dfrac{1}{(\dfrac{\sqrt{2}}{2})^2} = \dfrac{1}{\dfrac{1}{2}} = 2$。
首先，我们需要求出函数$f(x)=\tan x$的导数$f'(x)$。根据导数的定义和三角函数的导数公式，我们知道$\tan x$的导数是$\sec^2 x$，即$f'(x)=\sec^2 x$。
步骤 2：代入求值
接下来，我们需要计算$f'(\dfrac {\pi }{4})$的值。根据步骤1中得到的导数公式，我们只需将$x=\dfrac {\pi }{4}$代入$f'(x)=\sec^2 x$中。
步骤 3：计算结果
由于$\sec x = \dfrac{1}{\cos x}$，所以$\sec^2 x = \dfrac{1}{\cos^2 x}$。当$x=\dfrac {\pi }{4}$时，$\cos \dfrac {\pi }{4} = \dfrac{\sqrt{2}}{2}$，因此$\sec^2 \dfrac {\pi }{4} = \dfrac{1}{(\dfrac{\sqrt{2}}{2})^2} = \dfrac{1}{\dfrac{1}{2}} = 2$。