题目
1、设函数 f(x)= ) x|x|,xleqslant 0 xln x,xgt 0 . 则 x=0 是f(x)的A.可导点,极值点B.不可导点,极值点C.可导点,非极值点D.不可导点,非极值点
1、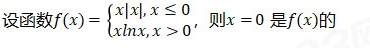
A.可导点,极值点
B.不可导点,极值点
C.可导点,非极值点
D.不可导点,非极值点
题目解答
答案
参考答案:B
参考解析:

解析
步骤 1:计算左导数
当 $x\leqslant 0$ 时,$f(x)=x|x|=x(-x)=-x^2$,因此 $f'(x)=-2x$。当 $x=0$ 时,左导数为 $f'(0^-)=-2\cdot0=0$。
步骤 2:计算右导数
当 $x\gt 0$ 时,$f(x)=x\ln x$,因此 $f'(x)=\ln x+1$。当 $x=0$ 时,右导数为 $f'(0^+)=\lim_{x\to0^+}(\ln x+1)$,由于 $\ln x$ 在 $x\to0^+$ 时趋于负无穷,因此右导数不存在。
步骤 3:判断极值点
当 $x\leqslant 0$ 时,$f'(x)=-2x\leqslant 0$,函数单调递减;当 $x\gt 0$ 时,$f'(x)=\ln x+1\gt 0$,函数单调递增。因此,$x=0$ 是函数的极值点。
当 $x\leqslant 0$ 时,$f(x)=x|x|=x(-x)=-x^2$,因此 $f'(x)=-2x$。当 $x=0$ 时,左导数为 $f'(0^-)=-2\cdot0=0$。
步骤 2:计算右导数
当 $x\gt 0$ 时,$f(x)=x\ln x$,因此 $f'(x)=\ln x+1$。当 $x=0$ 时,右导数为 $f'(0^+)=\lim_{x\to0^+}(\ln x+1)$,由于 $\ln x$ 在 $x\to0^+$ 时趋于负无穷,因此右导数不存在。
步骤 3:判断极值点
当 $x\leqslant 0$ 时,$f'(x)=-2x\leqslant 0$,函数单调递减;当 $x\gt 0$ 时,$f'(x)=\ln x+1\gt 0$,函数单调递增。因此,$x=0$ 是函数的极值点。