题目

求(x)=(e)^dfrac (1{{x)^2}}arctan dfrac ({x)^2+x-1}((x+1)(x-2))的间断点并判断其类型.

求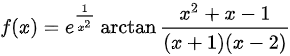 $f(x)=e^{\frac{1}{x^2}}\arctan\frac{x^2+x-1}{(x+1)(x-2)}$ 的间断点并判断其类型.

题目解答

答案

解：

$\begin{aligned} f(x) =&e^ {\frac{1} {x^2} } \arctan \frac {x^2+x-1} { (x+1) (x-2) } \\&根据基本函数y=\frac{1} {x}定义域为x\ne 0 \\&y=e^ {x}定义域为R \\&y=\arctan x定义域为R \\&可知f(x)定义域为x^2\ne 0，(x+1) (x-2)\ne 0 \\&解得x\ne 0，x\ne -1，x\ne 2 \\&即f(x)间断点为x=-1,0,2 \\&\lim_{x \to 0^+}\arctan \frac {x^2+x-1} { (x+1) (x-2) } =\lim_{x \to 0^-} \arctan \frac {x^2+x-1} { (x+1) (x-2) }=\arctan \frac{1}{2} \\&x\longrightarrow 0^+时\frac{1} {x^2}\longrightarrow+\infty ， e^ {\frac{1} {x^2} }\longrightarrow+\infty，即\lim_{x \to 0^+} e^ {\frac{1} {x^2} }=+\infty \\&x\longrightarrow 0^+时\frac{1} {x^2}\longrightarrow-\infty ， e^ {\frac{1} {x^2} }\longrightarrow0，即\lim_{x \to 0^+} e^ {\frac{1} {x^2} }=0 \\&即\lim_{x \to 0^+}f(x)=+\infty\bullet\arctan \frac{1}{2} = +\infty \\&\lim_{x \to 0^-}f(x)=0\bullet\arctan \frac{1}{2} = 0 \\&x=0为其无穷间断点 \\&\lim_{x \to -1^+}e^ {\frac{1} {x^2} }=\lim_{x \to -1^-}e^ {\frac{1} {x^2} }=e^ {\frac{1} {(-1)^2} }=e \\&x\longrightarrow -1^+时 \frac {x^2+x-1} { (x+1) (x-2) }\longrightarrow+\infty ， \\&\arctan \frac {x^2+x-1} { (x+1) (x-2) }\longrightarrow+\frac{\pi }{2} ，即\lim_{x \to -1^+} \arctan \frac {x^2+x-1} { (x+1) (x-2) }=+\frac{\pi }{2} \\&x\longrightarrow -1^-时 \frac {x^2+x-1} { (x+1) (x-2) }\longrightarrow-\infty ， \\&\arctan \frac {x^2+x-1} { (x+1) (x-2) }\longrightarrow-\frac{\pi }{2} ，即\lim_{x \to -1^-} \arctan \frac {x^2+x-1} { (x+1) (x-2) }=-\frac{\pi }{2} \end{aligned}$

$\begin{aligned} \\&即\lim_{x \to -1^+}f(x)=e\bullet (+\frac{\pi }{2})=e\frac{\pi }{2} \\&\lim_{x \to -1^-}f(x)=e\bullet (-\frac{\pi }{2})=-e\frac{\pi }{2} \\&同理得出\lim_{x \to 2^+}f(x)=e^{ \frac{1}{4}}\bullet (+\frac{\pi }{2})=e^{ \frac{1}{4}} \frac{\pi }{2} \\&\lim_{x \to 2^-}f(x)=e^{ \frac{1}{4}}\bullet (-\frac{\pi }{2})=-e^{ \frac{1}{4}} \frac{\pi }{2} \\&故x=-1，2为其跳跃间断点 \end{aligned}$

解析

步骤 1：确定函数的定义域
函数$f(x)={e}^{\dfrac {1}{{x}^{2}}}\arctan \dfrac {{x}^{2}+x-1}{(x+1)(x-2)}$中，${e}^{\dfrac {1}{{x}^{2}}}$在$x\neq 0$时有定义，$\arctan \dfrac {{x}^{2}+x-1}{(x+1)(x-2)}$在$x\neq -1$和$x\neq 2$时有定义。因此，函数$f(x)$在$x\neq 0$，$x\neq -1$，$x\neq 2$时有定义。

步骤 2：分析间断点
函数$f(x)$在$x=0$，$x=-1$，$x=2$处没有定义，因此这些点是函数的间断点。

步骤 3：判断间断点的类型
- 对于$x=0$，由于${e}^{\dfrac {1}{{x}^{2}}}$在$x=0$处的极限不存在，因此$x=0$是$f(x)$的第二类间断点。
- 对于$x=-1$和$x=2$，由于$\arctan \dfrac {{x}^{2}+x-1}{(x+1)(x-2)}$在$x=-1$和$x=2$处的极限存在，因此$x=-1$和$x=2$是$f(x)$的第一类间断点。