题目
9.计算: lim _(narrow infty )[ dfrac (1)(1times 4)+dfrac (1)(4times 7)+dfrac (1)(7times 10)+... +dfrac (1)((3n-2)(3n+1))] .
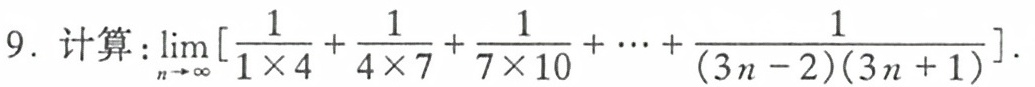
题目解答
答案
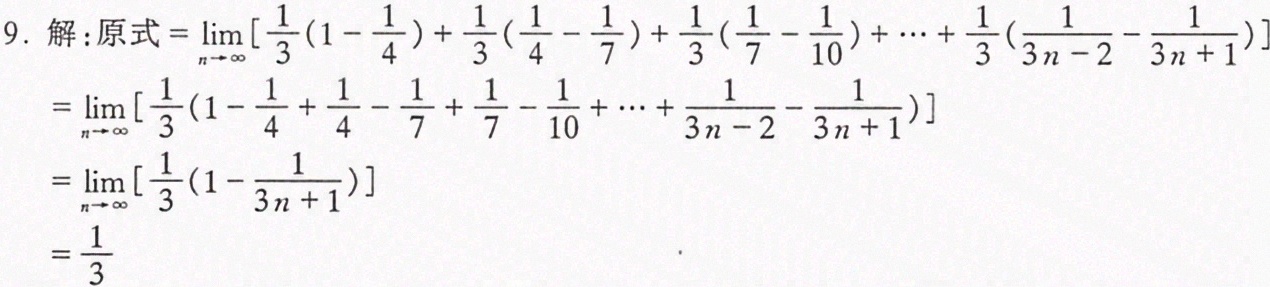
解析
步骤 1:观察通项
观察给定的序列,每一项可以表示为 $\dfrac{1}{(3k-2)(3k+1)}$,其中 $k$ 从 $1$ 开始递增。
步骤 2:部分分式分解
将每一项进行部分分式分解,即 $\dfrac{1}{(3k-2)(3k+1)} = \dfrac{A}{3k-2} + \dfrac{B}{3k+1}$。通过解方程组,可以得到 $A = \dfrac{1}{3}$,$B = -\dfrac{1}{3}$。因此,每一项可以写成 $\dfrac{1}{3}(\dfrac{1}{3k-2} - \dfrac{1}{3k+1})$。
步骤 3:求和
将每一项的分解形式相加,得到 $\dfrac{1}{3}[(1-\dfrac{1}{4})+(\dfrac{1}{4}-\dfrac{1}{7})+(\dfrac{1}{7}-\dfrac{1}{10})+\cdots+(\dfrac{1}{3n-2}-\dfrac{1}{3n+1})]$。这是一个部分和,其中大部分项相互抵消,只剩下 $1$ 和 $-\dfrac{1}{3n+1}$。
步骤 4:求极限
当 $n$ 趋向于无穷大时,$-\dfrac{1}{3n+1}$ 趋向于 $0$。因此,整个序列的极限为 $\dfrac{1}{3}$。
观察给定的序列,每一项可以表示为 $\dfrac{1}{(3k-2)(3k+1)}$,其中 $k$ 从 $1$ 开始递增。
步骤 2:部分分式分解
将每一项进行部分分式分解,即 $\dfrac{1}{(3k-2)(3k+1)} = \dfrac{A}{3k-2} + \dfrac{B}{3k+1}$。通过解方程组,可以得到 $A = \dfrac{1}{3}$,$B = -\dfrac{1}{3}$。因此,每一项可以写成 $\dfrac{1}{3}(\dfrac{1}{3k-2} - \dfrac{1}{3k+1})$。
步骤 3:求和
将每一项的分解形式相加,得到 $\dfrac{1}{3}[(1-\dfrac{1}{4})+(\dfrac{1}{4}-\dfrac{1}{7})+(\dfrac{1}{7}-\dfrac{1}{10})+\cdots+(\dfrac{1}{3n-2}-\dfrac{1}{3n+1})]$。这是一个部分和,其中大部分项相互抵消,只剩下 $1$ 和 $-\dfrac{1}{3n+1}$。
步骤 4:求极限
当 $n$ 趋向于无穷大时,$-\dfrac{1}{3n+1}$ 趋向于 $0$。因此,整个序列的极限为 $\dfrac{1}{3}$。