题目
[例4] 设 varphi (x)= { ,xneq 0 0, x=0 . 函数f(x)可导,求 (x)=f(varphi (x)) 的导数.

题目解答
答案
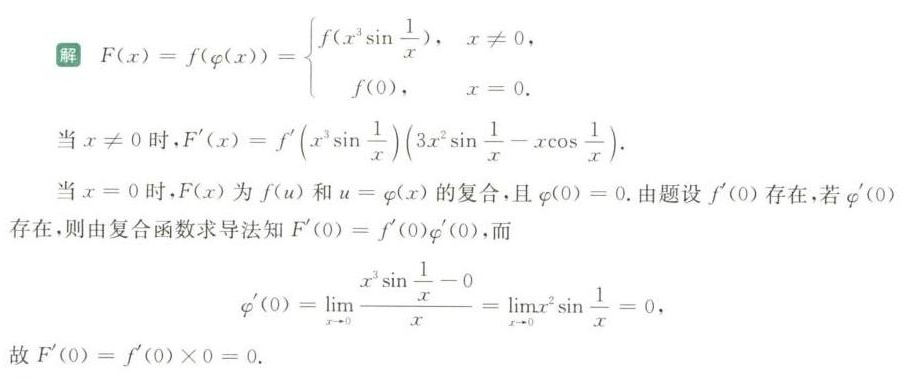
解析
步骤 1:定义函数 $F(x)$
函数 $F(x)$ 定义为 $F(x) = f(\varphi(x))$,其中 $\varphi(x)$ 是一个分段函数,定义如下:
$$
\varphi(x) = \begin{cases}
x^3 \sin \frac{1}{x}, & x \neq 0 \\
0, & x = 0
\end{cases}
$$
步骤 2:求 $F(x)$ 在 $x \neq 0$ 时的导数
当 $x \neq 0$ 时,$F(x) = f(x^3 \sin \frac{1}{x})$,根据复合函数求导法则,有:
$$
F'(x) = f'(x^3 \sin \frac{1}{x}) \cdot \frac{d}{dx}(x^3 \sin \frac{1}{x})
$$
计算 $\frac{d}{dx}(x^3 \sin \frac{1}{x})$:
$$
\frac{d}{dx}(x^3 \sin \frac{1}{x}) = 3x^2 \sin \frac{1}{x} - x^3 \cos \frac{1}{x} \cdot \frac{1}{x^2} = 3x^2 \sin \frac{1}{x} - x \cos \frac{1}{x}
$$
因此,当 $x \neq 0$ 时,$F'(x)$ 为:
$$
F'(x) = f'(x^3 \sin \frac{1}{x}) \cdot (3x^2 \sin \frac{1}{x} - x \cos \frac{1}{x})
$$
步骤 3:求 $F(x)$ 在 $x = 0$ 时的导数
当 $x = 0$ 时,$F(x) = f(0)$,根据复合函数求导法则,有:
$$
F'(0) = f'(0) \cdot \varphi'(0)
$$
计算 $\varphi'(0)$:
$$
\varphi'(0) = \lim_{x \to 0} \frac{\varphi(x) - \varphi(0)}{x} = \lim_{x \to 0} \frac{x^3 \sin \frac{1}{x}}{x} = \lim_{x \to 0} x^2 \sin \frac{1}{x} = 0
$$
因此,当 $x = 0$ 时,$F'(0)$ 为:
$$
F'(0) = f'(0) \cdot 0 = 0
$$
函数 $F(x)$ 定义为 $F(x) = f(\varphi(x))$,其中 $\varphi(x)$ 是一个分段函数,定义如下:
$$
\varphi(x) = \begin{cases}
x^3 \sin \frac{1}{x}, & x \neq 0 \\
0, & x = 0
\end{cases}
$$
步骤 2:求 $F(x)$ 在 $x \neq 0$ 时的导数
当 $x \neq 0$ 时,$F(x) = f(x^3 \sin \frac{1}{x})$,根据复合函数求导法则,有:
$$
F'(x) = f'(x^3 \sin \frac{1}{x}) \cdot \frac{d}{dx}(x^3 \sin \frac{1}{x})
$$
计算 $\frac{d}{dx}(x^3 \sin \frac{1}{x})$:
$$
\frac{d}{dx}(x^3 \sin \frac{1}{x}) = 3x^2 \sin \frac{1}{x} - x^3 \cos \frac{1}{x} \cdot \frac{1}{x^2} = 3x^2 \sin \frac{1}{x} - x \cos \frac{1}{x}
$$
因此,当 $x \neq 0$ 时,$F'(x)$ 为:
$$
F'(x) = f'(x^3 \sin \frac{1}{x}) \cdot (3x^2 \sin \frac{1}{x} - x \cos \frac{1}{x})
$$
步骤 3:求 $F(x)$ 在 $x = 0$ 时的导数
当 $x = 0$ 时,$F(x) = f(0)$,根据复合函数求导法则,有:
$$
F'(0) = f'(0) \cdot \varphi'(0)
$$
计算 $\varphi'(0)$:
$$
\varphi'(0) = \lim_{x \to 0} \frac{\varphi(x) - \varphi(0)}{x} = \lim_{x \to 0} \frac{x^3 \sin \frac{1}{x}}{x} = \lim_{x \to 0} x^2 \sin \frac{1}{x} = 0
$$
因此,当 $x = 0$ 时,$F'(0)$ 为:
$$
F'(0) = f'(0) \cdot 0 = 0
$$