题目
求微分方程'+y=x+1的通解。
求微分方程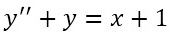 的通解。
的通解。
题目解答
答案

解析
步骤 1:求解齐次方程的通解
微分方程 $y''+y=0$ 的特征方程为 ${r}^{2}+1=0$,其根为 ${r}_{1}=i$ 和 ${r}_{2}=-i$,所以齐次方程的通解为 $y={C}_{1}\cos x+{C}_{2}\sin x$。
步骤 2:寻找非齐次方程的特解
由于非齐次项为 $x+1$,我们假设特解形式为 $y_p=ax+b$。将 $y_p$ 代入原方程,得到 $a(x+1)+ax+b=x+1$。通过比较系数,得到 $a=1$ 和 $b=0$,因此特解为 $y_p=x$。
步骤 3:写出原方程的通解
原方程的通解为齐次方程的通解加上非齐次方程的特解,即 $y={C}_{1}\cos x+{C}_{2}\sin x+x$。
微分方程 $y''+y=0$ 的特征方程为 ${r}^{2}+1=0$,其根为 ${r}_{1}=i$ 和 ${r}_{2}=-i$,所以齐次方程的通解为 $y={C}_{1}\cos x+{C}_{2}\sin x$。
步骤 2:寻找非齐次方程的特解
由于非齐次项为 $x+1$,我们假设特解形式为 $y_p=ax+b$。将 $y_p$ 代入原方程,得到 $a(x+1)+ax+b=x+1$。通过比较系数,得到 $a=1$ 和 $b=0$,因此特解为 $y_p=x$。
步骤 3:写出原方程的通解
原方程的通解为齐次方程的通解加上非齐次方程的特解,即 $y={C}_{1}\cos x+{C}_{2}\sin x+x$。