题目
设[x]是表示不超过x的最大整数,则 =x-[ x] 是 __-|||-(A)无界函数 (B)周期为1的周期函数 (C)单调函数 (D)偶函数

题目解答
答案
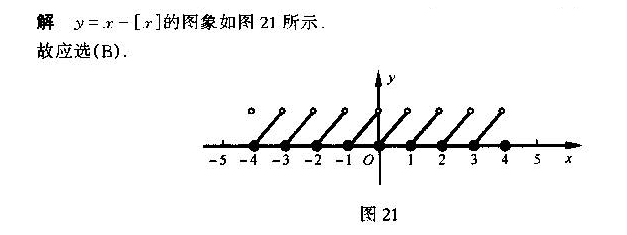
解析
步骤 1:理解函数 $y=x-[ x] $ 的定义
函数 $y=x-[ x] $ 表示的是 $x$ 减去不超过 $x$ 的最大整数,即 $x$ 减去 $x$ 的整数部分。因此,$y$ 的值域为 $[0,1)$,因为 $[x]$ 是 $x$ 的整数部分,$x-[x]$ 就是 $x$ 的小数部分。
步骤 2:分析函数的性质
- 无界函数:函数的值域为 $[0,1)$,因此函数是有界的,不是无界函数。
- 周期为1的周期函数:对于任意整数 $n$,有 $y(x+n) = (x+n) - [x+n] = x - [x] = y(x)$,因此函数是周期为1的周期函数。
- 单调函数:函数在每个整数区间 $[n, n+1)$ 内是单调递增的,但在整数点处不连续,因此不是单调函数。
- 偶函数:函数在 $x$ 和 $-x$ 处的值不相等,因此不是偶函数。
步骤 3:选择正确答案
根据上述分析,函数 $y=x-[ x] $ 是周期为1的周期函数。
函数 $y=x-[ x] $ 表示的是 $x$ 减去不超过 $x$ 的最大整数,即 $x$ 减去 $x$ 的整数部分。因此,$y$ 的值域为 $[0,1)$,因为 $[x]$ 是 $x$ 的整数部分,$x-[x]$ 就是 $x$ 的小数部分。
步骤 2:分析函数的性质
- 无界函数:函数的值域为 $[0,1)$,因此函数是有界的,不是无界函数。
- 周期为1的周期函数:对于任意整数 $n$,有 $y(x+n) = (x+n) - [x+n] = x - [x] = y(x)$,因此函数是周期为1的周期函数。
- 单调函数:函数在每个整数区间 $[n, n+1)$ 内是单调递增的,但在整数点处不连续,因此不是单调函数。
- 偶函数:函数在 $x$ 和 $-x$ 处的值不相等,因此不是偶函数。
步骤 3:选择正确答案
根据上述分析,函数 $y=x-[ x] $ 是周期为1的周期函数。