题目
(12)当x→1时, (x)=dfrac (1-x)(1+x) 与 (x)=1-sqrt [3](x) 比较,会得出什么样的结论?(2018年
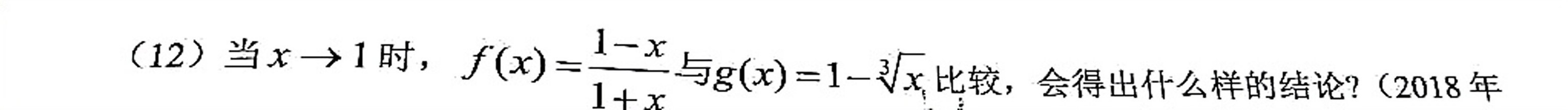
题目解答
答案

解析
步骤 1:确定极限形式
首先,我们需要确定当 $x \rightarrow 1$ 时,$f(x)$ 和 $g(x)$ 的极限形式。$f(x) = \dfrac{1-x}{1+x}$ 和 $g(x) = 1 - \sqrt[3]{x}$。
步骤 2:计算 $f(x)$ 的极限
计算 $f(x)$ 的极限,当 $x \rightarrow 1$ 时,$f(x) = \dfrac{1-x}{1+x} \rightarrow \dfrac{1-1}{1+1} = 0$。
步骤 3:计算 $g(x)$ 的极限
计算 $g(x)$ 的极限,当 $x \rightarrow 1$ 时,$g(x) = 1 - \sqrt[3]{x} \rightarrow 1 - \sqrt[3]{1} = 0$。
步骤 4:比较 $f(x)$ 和 $g(x)$ 的极限
由于 $f(x)$ 和 $g(x)$ 的极限都是 $0$,我们需要进一步比较它们的高阶无穷小量。为此,我们计算 $\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)}$。
步骤 5:计算 $\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)}$
$\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)} = \lim_{x \rightarrow 1} \dfrac{\dfrac{1-x}{1+x}}{1-\sqrt[3]{x}} = \lim_{x \rightarrow 1} \dfrac{1-x}{(1+x)(1-\sqrt[3]{x})}$。
步骤 6:使用立方差公式
使用立方差公式 $1 - x = (1 - \sqrt[3]{x})(1 + \sqrt[3]{x} + \sqrt[3]{x^2})$,我们得到:
$\lim_{x \rightarrow 1} \dfrac{1-x}{(1+x)(1-\sqrt[3]{x})} = \lim_{x \rightarrow 1} \dfrac{(1 - \sqrt[3]{x})(1 + \sqrt[3]{x} + \sqrt[3]{x^2})}{(1+x)(1-\sqrt[3]{x})} = \lim_{x \rightarrow 1} \dfrac{1 + \sqrt[3]{x} + \sqrt[3]{x^2}}{1+x}$。
步骤 7:计算最终极限
$\lim_{x \rightarrow 1} \dfrac{1 + \sqrt[3]{x} + \sqrt[3]{x^2}}{1+x} = \dfrac{1 + 1 + 1}{1+1} = \dfrac{3}{2}$。
首先,我们需要确定当 $x \rightarrow 1$ 时,$f(x)$ 和 $g(x)$ 的极限形式。$f(x) = \dfrac{1-x}{1+x}$ 和 $g(x) = 1 - \sqrt[3]{x}$。
步骤 2:计算 $f(x)$ 的极限
计算 $f(x)$ 的极限,当 $x \rightarrow 1$ 时,$f(x) = \dfrac{1-x}{1+x} \rightarrow \dfrac{1-1}{1+1} = 0$。
步骤 3:计算 $g(x)$ 的极限
计算 $g(x)$ 的极限,当 $x \rightarrow 1$ 时,$g(x) = 1 - \sqrt[3]{x} \rightarrow 1 - \sqrt[3]{1} = 0$。
步骤 4:比较 $f(x)$ 和 $g(x)$ 的极限
由于 $f(x)$ 和 $g(x)$ 的极限都是 $0$,我们需要进一步比较它们的高阶无穷小量。为此,我们计算 $\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)}$。
步骤 5:计算 $\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)}$
$\lim_{x \rightarrow 1} \dfrac{f(x)}{g(x)} = \lim_{x \rightarrow 1} \dfrac{\dfrac{1-x}{1+x}}{1-\sqrt[3]{x}} = \lim_{x \rightarrow 1} \dfrac{1-x}{(1+x)(1-\sqrt[3]{x})}$。
步骤 6:使用立方差公式
使用立方差公式 $1 - x = (1 - \sqrt[3]{x})(1 + \sqrt[3]{x} + \sqrt[3]{x^2})$,我们得到:
$\lim_{x \rightarrow 1} \dfrac{1-x}{(1+x)(1-\sqrt[3]{x})} = \lim_{x \rightarrow 1} \dfrac{(1 - \sqrt[3]{x})(1 + \sqrt[3]{x} + \sqrt[3]{x^2})}{(1+x)(1-\sqrt[3]{x})} = \lim_{x \rightarrow 1} \dfrac{1 + \sqrt[3]{x} + \sqrt[3]{x^2}}{1+x}$。
步骤 7:计算最终极限
$\lim_{x \rightarrow 1} \dfrac{1 + \sqrt[3]{x} + \sqrt[3]{x^2}}{1+x} = \dfrac{1 + 1 + 1}{1+1} = \dfrac{3}{2}$。