题目
设 lim _(xarrow 0)dfrac (ln (1+x)-(ax+b{x)^2)}({x)^2}=2, 则设 lim _(xarrow 0)dfrac (ln (1+x)-(ax+b{x)^2)}({x)^2}=2, 则
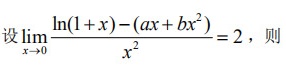

题目解答
答案
解析:

解析
步骤 1:利用洛必达法则
由于极限的形式为 $\frac{0}{0}$,我们可以使用洛必达法则。首先,对分子和分母分别求导。
分子的导数为 $\frac{d}{dx}[\ln(1+x) - (ax + bx^2)] = \frac{1}{1+x} - a - 2bx$。
分母的导数为 $\frac{d}{dx}[x^2] = 2x$。
步骤 2:应用洛必达法则
应用洛必达法则,我们得到 $\lim_{x\rightarrow 0} \frac{\frac{1}{1+x} - a - 2bx}{2x}$。
步骤 3:再次应用洛必达法则
由于极限的形式仍然为 $\frac{0}{0}$,我们再次应用洛必达法则。分子的导数为 $\frac{d}{dx}[\frac{1}{1+x} - a - 2bx] = -\frac{1}{(1+x)^2} - 2b$。
分母的导数为 $\frac{d}{dx}[2x] = 2$。
步骤 4:计算极限
应用洛必达法则,我们得到 $\lim_{x\rightarrow 0} \frac{-\frac{1}{(1+x)^2} - 2b}{2} = \frac{-1 - 2b}{2} = 2$。
步骤 5:解方程
解方程 $\frac{-1 - 2b}{2} = 2$,得到 $-1 - 2b = 4$,从而 $b = -\frac{5}{2}$。
步骤 6:确定 $a$ 的值
由于在步骤 1 中,分子的导数为 $\frac{1}{1+x} - a - 2bx$,当 $x\rightarrow 0$ 时,$\frac{1}{1+x} - a - 2bx$ 应该为 $0$,从而 $a = 1$。
由于极限的形式为 $\frac{0}{0}$,我们可以使用洛必达法则。首先,对分子和分母分别求导。
分子的导数为 $\frac{d}{dx}[\ln(1+x) - (ax + bx^2)] = \frac{1}{1+x} - a - 2bx$。
分母的导数为 $\frac{d}{dx}[x^2] = 2x$。
步骤 2:应用洛必达法则
应用洛必达法则,我们得到 $\lim_{x\rightarrow 0} \frac{\frac{1}{1+x} - a - 2bx}{2x}$。
步骤 3:再次应用洛必达法则
由于极限的形式仍然为 $\frac{0}{0}$,我们再次应用洛必达法则。分子的导数为 $\frac{d}{dx}[\frac{1}{1+x} - a - 2bx] = -\frac{1}{(1+x)^2} - 2b$。
分母的导数为 $\frac{d}{dx}[2x] = 2$。
步骤 4:计算极限
应用洛必达法则,我们得到 $\lim_{x\rightarrow 0} \frac{-\frac{1}{(1+x)^2} - 2b}{2} = \frac{-1 - 2b}{2} = 2$。
步骤 5:解方程
解方程 $\frac{-1 - 2b}{2} = 2$,得到 $-1 - 2b = 4$,从而 $b = -\frac{5}{2}$。
步骤 6:确定 $a$ 的值
由于在步骤 1 中,分子的导数为 $\frac{1}{1+x} - a - 2bx$,当 $x\rightarrow 0$ 时,$\frac{1}{1+x} - a - 2bx$ 应该为 $0$,从而 $a = 1$。