题目
已知曲线=a(x)^4+b(x)^3+(x)^2+3在点（1，6）处与直线=a(x)^4+b(x)^3+(x)^2+3相切，求a,b
已知曲线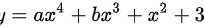
在点（1，6）处与直线
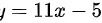相切，求a,b
题目解答
答案
由点（1，6）可知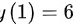
,即
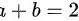
又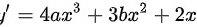
且直线的斜率为11，
即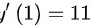
,得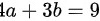
,
联立所得的两个方程：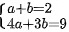
解得：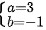
解析
步骤 1：确定曲线在点（1，6）处的函数值
曲线$y=a{x}^{4}+b{x}^{3}+{x}^{2}+3$在点（1，6）处，代入x=1，y=6，得到方程：
$6=a(1)^{4}+b(1)^{3}+(1)^{2}+3$
化简得：$a+b=2$
步骤 2：确定曲线在点（1，6）处的导数值
曲线$y=a{x}^{4}+b{x}^{3}+{x}^{2}+3$的导数为$y'=4a{x}^{3}+3b{x}^{2}+2x$
在点（1，6）处，导数$y'(1)=11$，代入x=1，得到方程：
$11=4a(1)^{3}+3b(1)^{2}+2(1)$
化简得：$4a+3b=9$
步骤 3：联立方程求解a和b
联立两个方程：
$\begin{cases} a+b=2 \\ 4a+3b=9 \end{cases}$
解得：$a=3$，$b=-1$
曲线$y=a{x}^{4}+b{x}^{3}+{x}^{2}+3$在点（1，6）处，代入x=1，y=6，得到方程：
$6=a(1)^{4}+b(1)^{3}+(1)^{2}+3$
化简得：$a+b=2$
步骤 2：确定曲线在点（1，6）处的导数值
曲线$y=a{x}^{4}+b{x}^{3}+{x}^{2}+3$的导数为$y'=4a{x}^{3}+3b{x}^{2}+2x$
在点（1，6）处，导数$y'(1)=11$，代入x=1，得到方程：
$11=4a(1)^{3}+3b(1)^{2}+2(1)$
化简得：$4a+3b=9$
步骤 3：联立方程求解a和b
联立两个方程：
$\begin{cases} a+b=2 \\ 4a+3b=9 \end{cases}$
解得：$a=3$，$b=-1$