题目
证明：lim _(narrow infty )(dfrac (1)({n)^2+n+1}+dfrac (2)({n)^2+n+2}+... +dfrac (n)({n)^2+n+n})=dfrac (1)(2)
证明：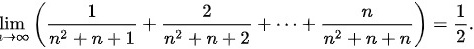
题目解答
答案
由于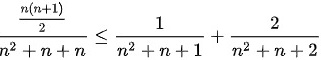
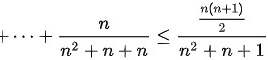.而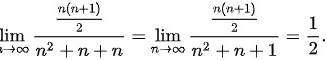
由夹逼准则可得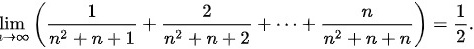故本题得证。
解析
步骤 1：确定序列的上下界
首先，我们注意到每一项 $\dfrac{k}{{n}^{2}+n+k}$ 都是正的，且随着 $k$ 的增加，分母增加，因此每一项都是递减的。我们可以通过比较每一项与序列的最小项和最大项来确定整个序列的上下界。
步骤 2：计算序列的下界
序列的最小项是 $\dfrac{1}{{n}^{2}+n+n}$，最大项是 $\dfrac{n}{{n}^{2}+n+1}$。因此，整个序列的和可以被下界 $\dfrac{1}{{n}^{2}+n+n} + \dfrac{2}{{n}^{2}+n+n} + \cdots + \dfrac{n}{{n}^{2}+n+n}$ 限制，即 $\dfrac{\dfrac{n(n+1)}{2}}{{n}^{2}+n+n}$。
步骤 3：计算序列的上界
同样地，整个序列的和可以被上界 $\dfrac{1}{{n}^{2}+n+1} + \dfrac{2}{{n}^{2}+n+1} + \cdots + \dfrac{n}{{n}^{2}+n+1}$ 限制，即 $\dfrac{\dfrac{n(n+1)}{2}}{{n}^{2}+n+1}$。
步骤 4：应用夹逼准则
由于 $\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n+n} = \lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n+1} = \dfrac {1}{2}$，根据夹逼准则，我们得出结论。
首先，我们注意到每一项 $\dfrac{k}{{n}^{2}+n+k}$ 都是正的，且随着 $k$ 的增加，分母增加，因此每一项都是递减的。我们可以通过比较每一项与序列的最小项和最大项来确定整个序列的上下界。
步骤 2：计算序列的下界
序列的最小项是 $\dfrac{1}{{n}^{2}+n+n}$，最大项是 $\dfrac{n}{{n}^{2}+n+1}$。因此，整个序列的和可以被下界 $\dfrac{1}{{n}^{2}+n+n} + \dfrac{2}{{n}^{2}+n+n} + \cdots + \dfrac{n}{{n}^{2}+n+n}$ 限制，即 $\dfrac{\dfrac{n(n+1)}{2}}{{n}^{2}+n+n}$。
步骤 3：计算序列的上界
同样地，整个序列的和可以被上界 $\dfrac{1}{{n}^{2}+n+1} + \dfrac{2}{{n}^{2}+n+1} + \cdots + \dfrac{n}{{n}^{2}+n+1}$ 限制，即 $\dfrac{\dfrac{n(n+1)}{2}}{{n}^{2}+n+1}$。
步骤 4：应用夹逼准则
由于 $\lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n+n} = \lim _{n\rightarrow \infty }\dfrac {\dfrac {n(n+1)}{2}}{{n}^{2}+n+1} = \dfrac {1}{2}$，根据夹逼准则，我们得出结论。