题目
2. (int )_(0)^+infty dfrac (x{e)^-x}({(1+{e)^-x)}^2}dx= ()-|||-__
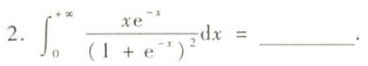
题目解答
答案
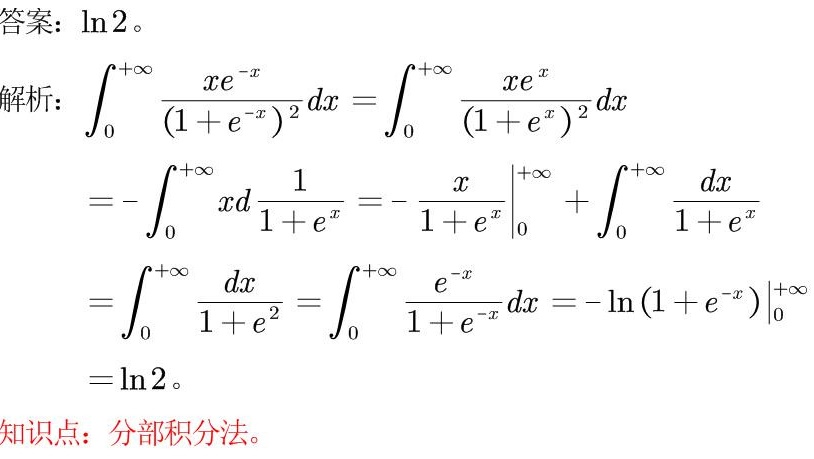
解析
步骤 1:换元法
令 $u = e^{-x}$,则 $du = -e^{-x}dx$,且当 $x = 0$ 时,$u = 1$;当 $x \to +\infty$ 时,$u \to 0$。因此,原积分可以写为:
$$
{\int }_{0}^{+\infty }\dfrac {x{e}^{-x}}{{(1+{e}^{-x})}^{2}}dx = -{\int }_{1}^{0}\dfrac {\ln u}{(1+u)^{2}}du = {\int }_{0}^{1}\dfrac {\ln u}{(1+u)^{2}}du
$$
步骤 2:分部积分法
设 $v = \ln u$,$dw = \dfrac {1}{(1+u)^{2}}du$,则 $dv = \dfrac {1}{u}du$,$w = -\dfrac {1}{1+u}$。根据分部积分法,有:
$$
{\int }_{0}^{1}\dfrac {\ln u}{(1+u)^{2}}du = \left[-\dfrac {\ln u}{1+u}\right]_{0}^{1} + {\int }_{0}^{1}\dfrac {1}{u(1+u)}du
$$
步骤 3:计算积分
计算上式中的积分,有:
$$
{\int }_{0}^{1}\dfrac {1}{u(1+u)}du = {\int }_{0}^{1}\left(\dfrac {1}{u} - \dfrac {1}{1+u}\right)du = \left[\ln u - \ln(1+u)\right]_{0}^{1} = \ln 2
$$
令 $u = e^{-x}$,则 $du = -e^{-x}dx$,且当 $x = 0$ 时,$u = 1$;当 $x \to +\infty$ 时,$u \to 0$。因此,原积分可以写为:
$$
{\int }_{0}^{+\infty }\dfrac {x{e}^{-x}}{{(1+{e}^{-x})}^{2}}dx = -{\int }_{1}^{0}\dfrac {\ln u}{(1+u)^{2}}du = {\int }_{0}^{1}\dfrac {\ln u}{(1+u)^{2}}du
$$
步骤 2:分部积分法
设 $v = \ln u$,$dw = \dfrac {1}{(1+u)^{2}}du$,则 $dv = \dfrac {1}{u}du$,$w = -\dfrac {1}{1+u}$。根据分部积分法,有:
$$
{\int }_{0}^{1}\dfrac {\ln u}{(1+u)^{2}}du = \left[-\dfrac {\ln u}{1+u}\right]_{0}^{1} + {\int }_{0}^{1}\dfrac {1}{u(1+u)}du
$$
步骤 3:计算积分
计算上式中的积分,有:
$$
{\int }_{0}^{1}\dfrac {1}{u(1+u)}du = {\int }_{0}^{1}\left(\dfrac {1}{u} - \dfrac {1}{1+u}\right)du = \left[\ln u - \ln(1+u)\right]_{0}^{1} = \ln 2
$$