题目
2.lim _(xarrow 0)(dfrac (2+{e)^dfrac (1{x)}}(1+{e)^dfrac (4{x)}}+dfrac (sin x)(|x|))
2.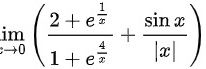
题目解答
答案
解:
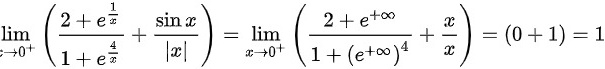
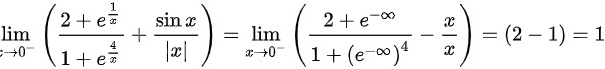
因为左右极限存在且相等,故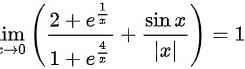
解析
步骤 1:分析极限的分段情况
由于极限中包含有 $\dfrac{1}{x}$ 和 $\dfrac{4}{x}$,我们需要分别考虑 $x$ 趋向于 $0^+$ 和 $0^-$ 的情况,因为这将影响到 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 的值。
步骤 2:计算 $x$ 趋向于 $0^+$ 的极限
当 $x$ 趋向于 $0^+$ 时,$\dfrac{1}{x}$ 和 $\dfrac{4}{x}$ 都趋向于 $+\infty$,因此 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 都趋向于 $+\infty$。此时,$\dfrac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}$ 的分子和分母都趋向于 $+\infty$,但分母的增长速度更快,因此该部分的极限为 $0$。同时,$\dfrac{\sin x}{|x|}$ 趋向于 $1$,因为 $\lim_{x\to 0} \dfrac{\sin x}{x} = 1$。因此,$x$ 趋向于 $0^+$ 时,整个表达式的极限为 $1$。
步骤 3:计算 $x$ 趋向于 $0^-$ 的极限
当 $x$ 趋向于 $0^-$ 时,$\dfrac{1}{x}$ 和 $\dfrac{4}{x}$ 都趋向于 $-\infty$,因此 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 都趋向于 $0$。此时,$\dfrac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}$ 的极限为 $\dfrac{2}{1} = 2$。同时,$\dfrac{\sin x}{|x|}$ 趋向于 $-1$,因为 $\lim_{x\to 0^-} \dfrac{\sin x}{x} = -1$。因此,$x$ 趋向于 $0^-$ 时,整个表达式的极限为 $2 - 1 = 1$。
步骤 4:判断极限是否存在
由于 $x$ 趋向于 $0^+$ 和 $0^-$ 时,整个表达式的极限都为 $1$,因此原极限存在且等于 $1$。
由于极限中包含有 $\dfrac{1}{x}$ 和 $\dfrac{4}{x}$,我们需要分别考虑 $x$ 趋向于 $0^+$ 和 $0^-$ 的情况,因为这将影响到 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 的值。
步骤 2:计算 $x$ 趋向于 $0^+$ 的极限
当 $x$ 趋向于 $0^+$ 时,$\dfrac{1}{x}$ 和 $\dfrac{4}{x}$ 都趋向于 $+\infty$,因此 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 都趋向于 $+\infty$。此时,$\dfrac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}$ 的分子和分母都趋向于 $+\infty$,但分母的增长速度更快,因此该部分的极限为 $0$。同时,$\dfrac{\sin x}{|x|}$ 趋向于 $1$,因为 $\lim_{x\to 0} \dfrac{\sin x}{x} = 1$。因此,$x$ 趋向于 $0^+$ 时,整个表达式的极限为 $1$。
步骤 3:计算 $x$ 趋向于 $0^-$ 的极限
当 $x$ 趋向于 $0^-$ 时,$\dfrac{1}{x}$ 和 $\dfrac{4}{x}$ 都趋向于 $-\infty$,因此 $e^{\frac{1}{x}}$ 和 $e^{\frac{4}{x}}$ 都趋向于 $0$。此时,$\dfrac{2+e^{\frac{1}{x}}}{1+e^{\frac{4}{x}}}$ 的极限为 $\dfrac{2}{1} = 2$。同时,$\dfrac{\sin x}{|x|}$ 趋向于 $-1$,因为 $\lim_{x\to 0^-} \dfrac{\sin x}{x} = -1$。因此,$x$ 趋向于 $0^-$ 时,整个表达式的极限为 $2 - 1 = 1$。
步骤 4:判断极限是否存在
由于 $x$ 趋向于 $0^+$ 和 $0^-$ 时,整个表达式的极限都为 $1$,因此原极限存在且等于 $1$。