题目
(8) lim _(xarrow 0)dfrac (1-cos 2x)(xln (1+x)) ;
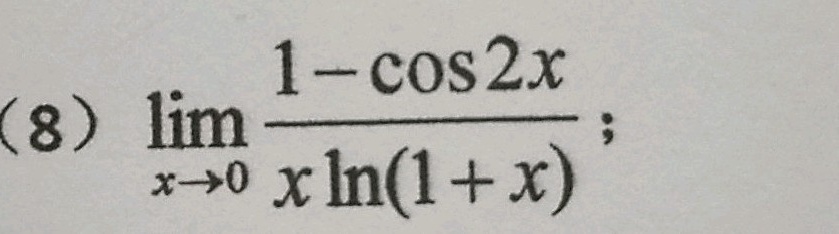
题目解答
答案
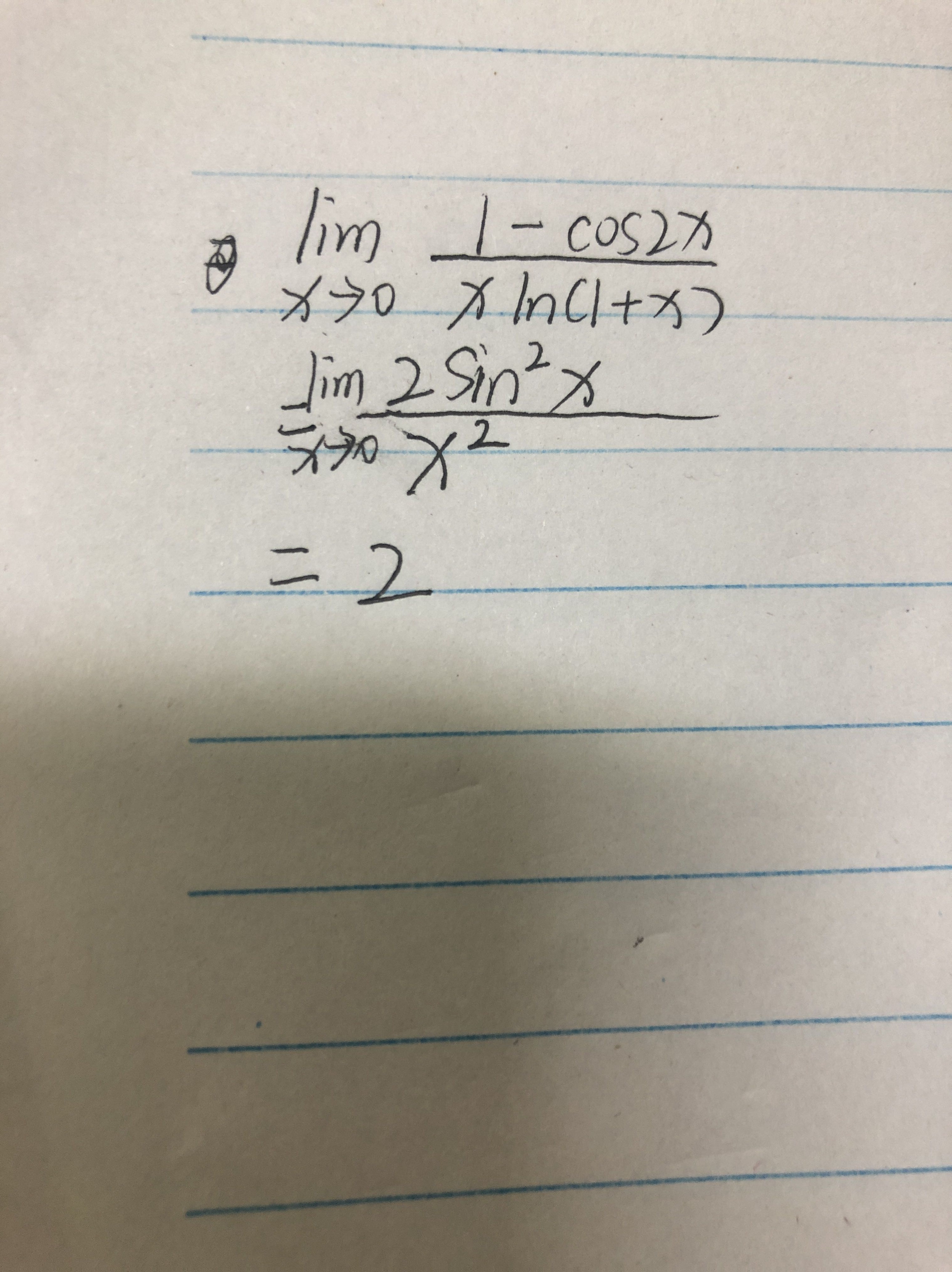
解析
步骤 1:使用三角恒等式
我们首先使用三角恒等式 $1-\cos 2x = 2\sin^2 x$ 来简化分子。
步骤 2:使用对数的性质
我们注意到分母中的 $\ln(1+x)$ 在 $x\rightarrow 0$ 时可以近似为 $x$,因为 $\ln(1+x) \approx x$ 当 $x$ 接近 $0$ 时。
步骤 3:计算极限
将上述两个步骤的结果代入原极限表达式中,然后计算极限。
我们首先使用三角恒等式 $1-\cos 2x = 2\sin^2 x$ 来简化分子。
步骤 2:使用对数的性质
我们注意到分母中的 $\ln(1+x)$ 在 $x\rightarrow 0$ 时可以近似为 $x$,因为 $\ln(1+x) \approx x$ 当 $x$ 接近 $0$ 时。
步骤 3:计算极限
将上述两个步骤的结果代入原极限表达式中,然后计算极限。