题目
2.已知函数 f(x)= { , xgt 0 a+cos x, xleqslant 0 . 在 x=0 处连续,求常数a的值.
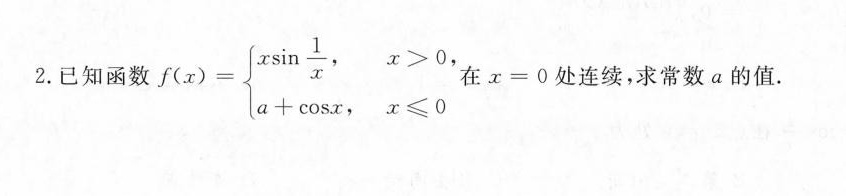
题目解答
答案
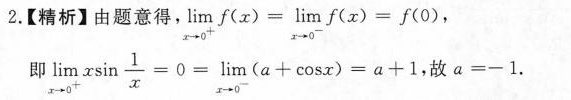
解析
步骤 1:确定函数在 x=0 处的左极限
函数在 x=0 处的左极限为 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{-}}(a+\cos x)=a+\cos 0=a+1$。
步骤 2:确定函数在 x=0 处的右极限
函数在 x=0 处的右极限为 $\lim _{x\rightarrow 0^{+}}f(x)=\lim _{x\rightarrow 0^{+}}x\sin \dfrac {1}{x}$。由于 $x\sin \dfrac {1}{x}$ 在 x=0 处的极限为 0,因此 $\lim _{x\rightarrow 0^{+}}x\sin \dfrac {1}{x}=0$。
步骤 3:根据函数在 x=0 处连续的条件
函数在 x=0 处连续,意味着左极限等于右极限,也等于函数在 x=0 处的值。因此,我们有 $a+1=0$。
步骤 4:求解常数a的值
解方程 $a+1=0$,得到 $a=-1$。
函数在 x=0 处的左极限为 $\lim _{x\rightarrow 0^{-}}f(x)=\lim _{x\rightarrow 0^{-}}(a+\cos x)=a+\cos 0=a+1$。
步骤 2:确定函数在 x=0 处的右极限
函数在 x=0 处的右极限为 $\lim _{x\rightarrow 0^{+}}f(x)=\lim _{x\rightarrow 0^{+}}x\sin \dfrac {1}{x}$。由于 $x\sin \dfrac {1}{x}$ 在 x=0 处的极限为 0,因此 $\lim _{x\rightarrow 0^{+}}x\sin \dfrac {1}{x}=0$。
步骤 3:根据函数在 x=0 处连续的条件
函数在 x=0 处连续,意味着左极限等于右极限,也等于函数在 x=0 处的值。因此,我们有 $a+1=0$。
步骤 4:求解常数a的值
解方程 $a+1=0$,得到 $a=-1$。