题目
lim _(xarrow {0)^-}(e)^dfrac (1{x)}=-|||-()
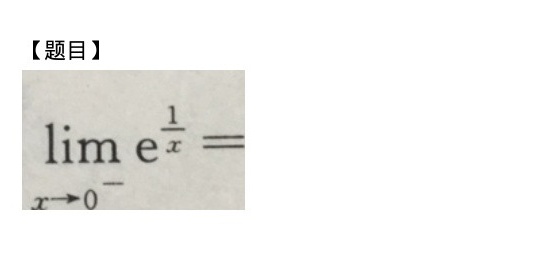
题目解答
答案
最佳答案

解析
步骤 1:分析函数行为
当 $x$ 趋向于 $0^{-}$ 时,$\dfrac{1}{x}$ 趋向于 $-\infty$。这是因为当 $x$ 是一个非常小的负数时,$\dfrac{1}{x}$ 将是一个非常大的负数。
步骤 2:应用指数函数的性质
指数函数 $e^x$ 在 $x$ 趋向于 $-\infty$ 时,其值趋向于 $0$。因此,当 $\dfrac{1}{x}$ 趋向于 $-\infty$ 时,$e^{\dfrac{1}{x}}$ 趋向于 $0$。
步骤 3:得出结论
根据上述分析,当 $x$ 趋向于 $0^{-}$ 时,$e^{\dfrac{1}{x}}$ 的极限值为 $0$。
当 $x$ 趋向于 $0^{-}$ 时,$\dfrac{1}{x}$ 趋向于 $-\infty$。这是因为当 $x$ 是一个非常小的负数时,$\dfrac{1}{x}$ 将是一个非常大的负数。
步骤 2:应用指数函数的性质
指数函数 $e^x$ 在 $x$ 趋向于 $-\infty$ 时,其值趋向于 $0$。因此,当 $\dfrac{1}{x}$ 趋向于 $-\infty$ 时,$e^{\dfrac{1}{x}}$ 趋向于 $0$。
步骤 3:得出结论
根据上述分析,当 $x$ 趋向于 $0^{-}$ 时,$e^{\dfrac{1}{x}}$ 的极限值为 $0$。